Задача
Какое наибольшее количество а) ладей; б) ферзей можно расставить на шахматной доске 8×8 так, чтобы каждая из этих фигур была под ударом не более чем одной из остальных?
Решение
а) Пусть k ладей расположены с соблюдением условия. На каждом поле, где стоит ладья, напишем число 0. В каждом из n столбцов проделаем следующую операцию: если в столбце стоят два числа, то прибавим к обоим по 1, если одно число, то к нему прибавим 2 (в пустом столбце ничего писать не будем). Затем проделаем точно такую же операцию с каждой строкой. Ясно, что на месте каждой из k ладей в результате будет написано либо 3, либо 4, поэтому сумма S всех написанных чисел не меньше 3k; с другой стороны, поскольку в каждый из восьми столбцов и затем в каждую из восьми строк мы добавили не более чем 2, то S ≤ 32. Итак, 3k ≤ S ≤ 4n, откуда k ≤ 10.
Пример расстановки 10 ладей, удовлетворяющей условию, показан на рисунке слева.
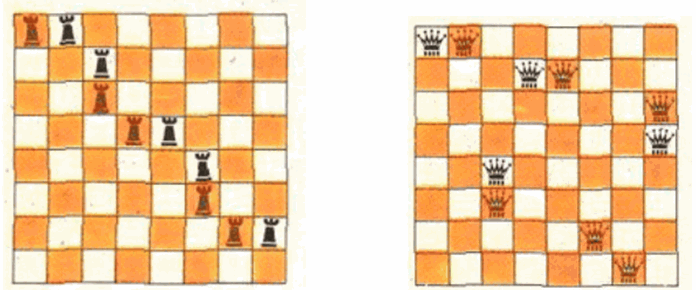
Ответ
а) 10 ладей, б) 10 ферзей.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь