Задача
На плоскости даны две точки A и B. Пусть C – некоторая точка плоскости, равноудалённая от точек A и B. Построим последовательность точек
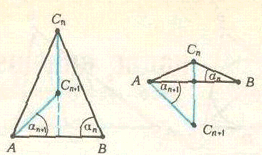
C1 = C, C2, C3, ..., где Cn+1 – центр описанной окружности треугольника ABCn. При каком положении точки C
а) точка Cn попадёт в середину отрезка AB (при этом Cn+1 и дальнейшие члены последовательности не определены)?
б) точка Cn совпадает с C?
Решение
Пусть ∠CnBA = ∠Cn AB = αn. Легко проверить (см. рис.), что для остроугольного треугольника αn+1 = 2αn – π/2, π/4 < αn < π/2, для тупоугольного
αn+1 = π/2 – 2αn, 0 < αn < π/4.
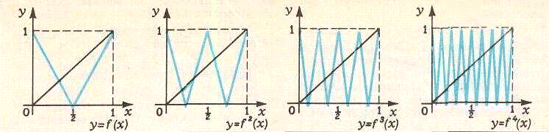
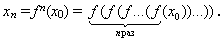 Заметим, что f(0) =f(1) = 1, f(½) = 0. Каждый из отрезков [0, ½], [½, 1] отображение fрастягивает вдвое и отображает на весь отрезок [0, 1] (см. рис.).
Заметим, что f(0) =f(1) = 1, f(½) = 0. Каждый из отрезков [0, ½], [½, 1] отображение fрастягивает вдвое и отображает на весь отрезок [0, 1] (см. рис.).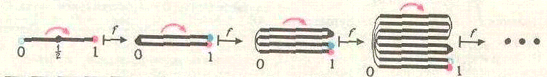
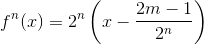 для
для 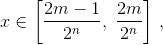
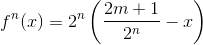 для
для 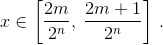
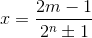 (m = 1, 2, 3, ..., 2n–1).
(m = 1, 2, 3, ..., 2n–1).
Ответ
а) При таком, что ∠CBA = pπ·2–n–1, где p – нечётное натуральное число, меньшее 2n.
б) При таком, что 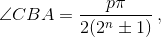 где p – нечётное натуральное число, p ≤ 2n – 1 (за исключением случая ∠CBA = π/2).
где p – нечётное натуральное число, p ≤ 2n – 1 (за исключением случая ∠CBA = π/2).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь