Задача
Король обошёл шахматную доску, побывав на каждом поле ровно один раз и вернувшись последним ходом на исходное поле. (Король ходит по обычным правилам: за один ход он может перейти по горизонтали, вертикали или диагонали на любое соседнее поле.) Когда нарисовали его путь, последовательно соединив центры полей, которые он проходил, получилась замкнутая ломаная без самопересечений. Какую наименьшую и какую наибольшую длину может она иметь? (Сторона клетки равна единице.)
Решение
Король сделал 64 хода. Поскольку длина каждого хода равна либо единице (прямой ход), либо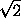 
  (диагональный ход), то длина всего пути заведомо не меньше 64. Путь длины 64 изображён на рисунке.
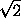. Рассмотрим два соседних выходаAиBкороля на границу доски. Если эти граничные поля не соседние, то участок пути короля между ними разбивает доску на две части, в каждой из которых есть целые клетки. Но тогда король не сможет пройти из одной части в другую, что противоречит условию. Значит, поляAиB– соседние и, следовательно, разного цвета. Так как при диагональных ходах цвет поля не меняется, то между каждыми двумя соседними выходами на границу должен быть прямой ход. Поскольку граничных полей 28, то и выходов на границу – тоже 28, и, следовательно, прямолинейных ходов не меньше 28. Следующий рисунок показывает,, что можно обойтись ровно 28 "прямыми" ходами.
Ответ
Наименьшая длина – 64, наибольшая – 28 + 36.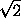
Чтобы оставлять комментарии, войдите или зарегистрируйтесь