Задача
n человек не знакомы между собой. Нужно так познакомить друг с другом некоторых из них, чтобы ни у каких трёх людей не оказалось одинакового числа знакомых. Докажите, что это можно сделать при любом n.
Решение
Решение 1: Индукция по n. База. При n < 3 конструкция очевидна.
Шаг индукции. Предположим, что удалось познакомить n человек, так, что никакие трое из них не имеют равного числа знакомых. Присоединим (n+1)-го. Если среди первых n человек найдётся человек, знакомый со всеми остальными, то (n+1)-го не будем ни с кем знакомить. Если же такого нет, то познакомим (n+1)-го со всеми.
В первом случае (n+1)-й не имеет знакомых, а каждый из остальных имеет хоть одного знакомого – того, который ранее был знаком со всеми. Во втором случае (n+1)-й имеет n знакомых, количество знакомых у каждого из первых n человек возросло на единицу, но ни у одного из них не стало n знакомых.
На рисунке показаны схемы знакомств при n ≤ 6, получающиеся описанным способом.
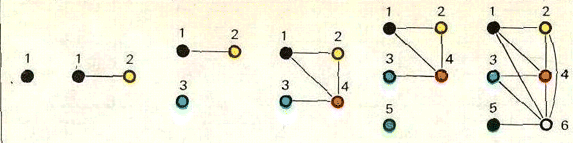
Решение 2: Занумеруем n человек числами от 1 до n и познакомим i-го с j-м, если |i – j| ≤ n/2. Тогда равное количество знакомых имеют только пары людей с номерами k и n – k (при k ≤ n/2 человек с номером k – 1 имеет, очевидно, на одного знакомого меньше, чем человек с номером k).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь