Многократно применяя равенство     запишем левую часть в виде 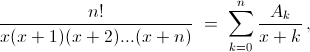    где A_k – некоторые числа. Умножим обе части на  x(x + 1)...(x + n)  и подставим  x = –k.  Тогда справа все слагаемые, кроме одного  A_k(–k)(–k + 1)...·(–1)·1·2·...(n – k) = A_k·(–1)^k·k!(n – k)!,  обратятся в нуль, и мы получаем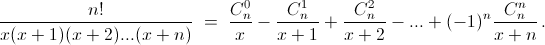  

Ответ задачи отсутствует