Пусть сначала n – не любое натуральное число, а заключено в промежутке

1 n N,

где N – заданное число. Тогда задача о минимизации максимального числа вопросов для отгадывания n известна.

Наилучшая в этом смысле стратегия, назовем ее S_n , состоит в том, что каждый новый вопрос делит промежуток значений, которые еще может принимать неизвестное пока число n , на две равные (или отличающиеся на 1) части. Именно, если мы уже знаем, что

a n < b,

то надо задать вопрос: "верно ли, что n "? Стратегия S_n описана.

Можно доказать, что максимальное число вопросов для отгадывания числа n N при использовании S_n равно ]log _{_}2 N[, где ]l[ означает наименьшее целое число, не меньшее l .

Ответим теперь на вопрос (б). Докажем, что для любой стратегии T и любого числа n

f'_T(n) ]log _{_}2 N[.

Доказательство. Пусть задано натуральное N , и неизвестное число n находится в промежутке от 1 до N . Пусть

2^m-1 2^m.

Тогда наибольший промежуток P₁ значений, которые еще может принимать n после первого вопроса, строго больше2^m-2(Разумеется, мы считаем, что "Злой Рок" (см."Квант" #8, 1972 г., с.4) помнит про свои обязанности.) , наибольший промежуток P₂ , в котором может находиться n после второго вопроса, больше2^m-3, и так далее. По индукции получаем, что наибольший промежуток P_m-1, в котором может находиться n после m-1-го вопроса, больше1. Значит, максимальное число вопросов (при наиболее неблагоприятных ответах) не меньше, чем Займемся вопросом (а)задачи M180. Пусть мы задали несколько вопросов типа "верно ли, что n x " и получали ответы "да": число n все время оказывалось больше или равно очередному x . Ясно, что следующее x надо взять больше всех уже употребленных (иначе этот вопрос будет лишним).

Таким образом, в начале игры надо все время увеличивать x – до тех пор, пока в первый раз загадавший не скажет "нет". Пусть x₁<x₂<x₃<... – последовательность, которую угадывающий решил называть, пока не получит первый ответ "нет". Она должна быть бесконечной, так как n может оказаться сколь угодно большим.

Пусть теперь наступил второй этап игры: на k -й вопрос загадавший в первый раз ответил "нет". Таким образом,

x_k-1 n<x_k.

Дальше можно применить стратегию, аналогичную описанной выше стратегии S_n , делить оставшийся промежуток все время пополам. Очевидно, при этом будет потрачено до]log _{_}2 (x_k-x_k-1)[вопросов.

Предположим, что на втором этапе игры, т.е. после первого ответа "нет", мы именно так и играем. Остается выбрать монотонно возрастающую последовательность x_k , чтобы полностью определить стратегию.

Разберем три конкретных стратегии, отличающиеся лишь выбором последовательности x_k .

1. Стратегия T¹ : x_k=10k . Тогда, как указано в условии, f_T(n) растет примерно как .

2. Стратегия T² : x_k=2^k . Тогда число вопросов на первом этапе не больше ]log 2 n[, а число вопросов на втором этапе не больше ]log 2 [. Всего получается примерно 2log _{_}2 n вопросов.

3. Стратегия T³ : x_k=22^k . Теперь число вопросов на первом этапе резко уменьшилось. В самом деле, пусть

Тогда число вопросов на первом этапе игры равно k и не превышает

k log 2 log 2 n+1,

что при больших n значительно меньше, чем log _{_}2 n . На втором этапе мы потратим приблизительно

log 2 (22^k-22^k-1) log 2 22^k=2^k

вопросов. Хорошо это или плохо? Это зависит от числа n . Оказывается, для наибольших n в промежутке(eq:180.2) эта стратегия значительно лучше, чем для наименьших n в том же промежутке.

Пусть n=22^k-1.

Тогда

f_T³(n) log 2 log 2 n+2^k log 2 n+log 2 log _{_}2 n.

При больших n второе слагаемое значительно меньше первого, и отношение f_T³(n) к нижней оценке log _{_}2 n (см.формулу(eq:180.1)) близко к1.

Пусть теперь n=22^k-1. Тогда величина f_T³(n)– такая же, а выраженная через n она составляет

f_T³(n) log 2 log 2 n+2^k 2log 2 n+log 2 log _{_}2 n,

т.е. примерно вдвое превышает нижнюю оценку(eq:180.1). Таким образом, для этих значений n стратегия T³ ничем не лучше стратегии T² .

Это положение иллюстрируется графиком на рис.7. На этом графике красная линия условно изображает доказанную выше нижнюю оценку: log _{_}2 n (график носит качественный, эскизный характер и не претендует на точность).

Ступенчатая черная линия изображает график функции f_T³(n). Эта функция постоянна на каждом промежутке вида(eq:180.2). К концу такого промежутка нижняя оценка почти догоняет ее, но тут f_T³(n) скачком увеличивается и делается примерно вдвое больше.

Возникает вопрос: существует ли такая стратегия T⁴ , для которой f_T⁴(n) при всех n не слишком сильно отличается от нижней оценки? (Предположительный график f_T⁴(n) приведен синим пунктиром.)

Сейчас мы опишем стратегию T⁴ такую, что

т.е. относительное превышение f_T⁴(n) над нижней оценкой log _{_}2 n при больших n стремится к нулю.

Первый этап игры, как и прежде, определяется последовательностью чисел

x_k=22^k.

Пусть на k -й вопрос мы в первый раз получили ответ "нет", откуда

22^k-1 n< 22^k.

Опишем стратегию T⁴ для второго этапа игры. Припишем каждому n в промежутке(eq:180.2) "вес", равный 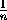. Будем теперь задавать вопросы так, чтобы делить примерно пополам не количество значений, которые еще может принимать n , а сумму их весов.

Подсчитаем примерно, сколько вопросов уйдет на отгадывание произвольного n в промежутке(eq:180.2). Положим m=22^k-1. Вначале сумма весов примерно равна

Если мы отгадаем n , то доведем сумму весов до величины 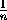. Значит, сумма весов уменьшится примерно в n ln n раз. Предположим, что нам каждый раз удавалось делить ее точно вдвое. Тогда было затрачено

log 2 n ln n=log 2 n+log 2 ln n log 2 n

вопросов (второе слагаемое при больших n значительно меньше первого). Поскольку сумму весов, как правило, точно разделить пополам не удастся, число вопросов фактически несколько больше. Можно показать (но это уже сложнее), что она все же не превышает

log 2 n+const log 2 log _{_}2 n

вопросов. (Здесьconst означает постоянное число, которое мы не оценивали.) Прибавляя сюда число вопросов на первом этапе игры, мы только увеличиваем коэффициент во втором слагаемом. Таким образом, мы построили стратегию, которая позволяет отгадать любое n не более чем за

log 2 n+const log 2 log _{_}2 n

вопросов.

Легко показать, что эта функция удовлетворяет условию(eq:180.3), которое мы и обещали выполнить.

Ответ задачи отсутствует