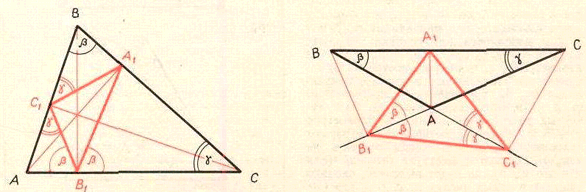
а) Пусть AA₁, BB₁ и CC₁ – высоты треугольника T. Углы α₁, β₁, γ₁ при вершинах A₁, B₁, C₁ (соответственно) треугольника A₁B₁C₁ выражаются через углы α, β, γ при вершинах A, B, C треугольника ABC следующим образом:

    α₁ = π – 2α,  β₁ = π – 2β,  γ₁ = π – 2γ,  если все углы острые;

    α₁ = 2α – π,  β₁ = 2β,  γ₁ = 2γ,  если   α > ^π/₂;

    α₁ = 2α,  β₁ = 2β – π,  если  β > ^π/₂;

    α₁ = 2α,  β₁ = 2β,  γ₁ = 2γ – π, если  γ > ^π/₂.   (1)

(см. рис.).

  Из формул (1) следует, что все три угла α₁, β₁, γ₁– острые в том и только в том случае, если выполнено одно из двух условий: либо все три угла α, β, γ заключены между^π/₄и^π/₂, либо два из них меньше^π/₄, а третий (тупой) меньше^3π/₄.   б) Заметим, что α₁ при данном α может равняться только одному из трёх чисел:  2α – π,  π – 2α  или 2α; соответственно α может равняться ½ (π + α₁);  ½ (π – α₁); или  ½ α₁.  Отсюда вытекает, что  α₁ = ^πk/_2^m  (k, m – некоторые целые числа) тогда и только тогда, когда  α = ^πl/_2^m+1  (l – некоторое целое число). Поэтому последовательность T₁, T₂, T₃, ... "вырождается" (некоторый треугольник T_n+1 оказывается прямоугольным) тогда и только тогда, когда один из углов α, β или γ равен ^πs/_2ⁿ, где s и n – некоторые натуральные числа.   в) Как будет видно из решения г), есть 56 вариантов таких треугольников. Перечислять их мы не будем.   г) Выясним, когда когда треугольник T_n подобен T. Начнём с  n = 1.  Для того чтобы треугольники с углами  (α₁, β₁, γ₁)  и  (α, β, γ)  были подобны, нужно, чтобы тройка чисел  (α₁, β₁, γ₁)  после некоторой перестановки совпала с  (α, β, γ).

  Ясно, что можно рассматривать только случай  α ≥ β ≥ γ.   (2)

  Если  α < ^π/₂  (все углы – острые), то, поскольку из (2) вытекают неравенства  2π – α ≤ 2π – β ≤ 2π – γ,  для подобия треугольников T₁ и T должна выполняться система равенств  π – 2α = γ,  π – 2β = β,  π – 2γ = α,  откуда   α = β = γ = ^π/₃.

  Если же α > ^π/₂,  то из (2) мы можем пользоваться только тем, что  2β ≥ 2γ,  и должны рассмотреть три возможных соотношения между углами α₁, β₁ и γ₁:  2β ≥ 2γ ≥ 2α – π,  2β ≥ 2α – π ≥ 2γ  и  2α – π ≥ 2β ≥ 2γ.  Первое из них приводит к системе  2β = α,  2γ = β,  2α – π = γ,  откуда находим еще одно решение:  α = ^4π/₇,  β = ^2π/₇,  γ = ^π/₇,  а два других приводят к "вырожденным" решениям (один из углов обращается в нуль).

  Перейдём к случаю произвольного n. Обозначим через  (α, β, γ), (α₁, β₁, γ₁), ..., (α_n, β_n, γ_n)  углы треугольника T и соответствующих ему треугольников T₁, ..., T_n. Требуется узнать, сколько существует троек  (α, β, γ),  для которых тройка  (α_n, β_n, γ_n)  совпадает с  (α, β, γ)  или получается из неё перестановкой, причём  α ≥ β ≥ γ.

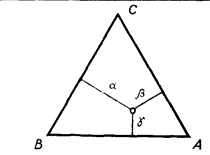
  Тройки  (α, β, γ)  и их преобразования  h: (α, β, γ) → (α₁, β₁, γ₁),  hⁿ: (α, β, γ) → (α_n, β_n, γ_n)  удобно представлять себе геометрически следующим образом. Нарисуем треугольник Y у которого длина каждой высоты равна π и будем изображать тройку неотрицательных чисел  (α, β, γ),  для которой  α + β + γ = π,  точкой y внутри этого треугольника, расстояния от которой до сторон равна соответственно α, β и γ(см. рис.).

  Такое соответствие между тройками  (α, β, γ)  и точкамиy∈Y  взаимно однозначно. Перестановке чисел в тройке  (α, β, γ) соответствуют перемещения треугольника, совмещающие его с самим собой (повороты и симметрии относительно высот). Преобразованиеhгеометрически описывается так. На средних линиях треугольникаY(точкамyсредних линий соответствуют прямоугольные треугольникиT)hне определено, а каждый из четырёх треугольников, на которые средние линии разбивают треугольникY,  hотображает на весьY, причём это отображение – преобразование подобия с коэффициентом 2, переводящее каждый отрезок в параллельный ему отрезок. 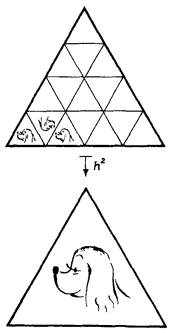Отсюда индукцией поnполучаем, что преобразованиеhⁿустроено аналогично: на прямых, параллельных сторонам и разбивающих высоты на 2ⁿравных частей,hⁿне определено; в каждом из 2²ⁿтреугольничков, на которые эти прямые разбиваютY  hⁿ– преобразование подобия с коэффициентом 2ⁿ, отображающее этот треугольничек на весьY. 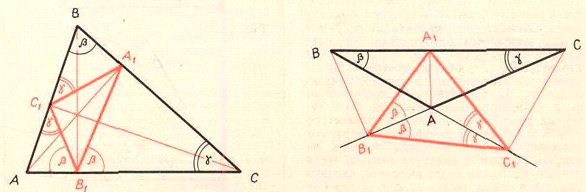(На рисунке изображеноh².)  Условия  α ≥ β ≥ γ  выделяют один из шести треугольников, на которые разбивают треугольникYего высоты. Этот прямоугольный треугольник обозначимY₁, остальные – как показано на рис. слева – обозначим соответственноY₂, ...,Y₆. Пусть  f_j:Y→Y– такое перемещениеY, что  f_j(Y_j) =Y₁.  Если каждый из 2²ⁿмаленьких треугольничков, которые отображаются преобразованиемhⁿна весь треугольникY, разбить высотами на шесть треугольников, тоY₁будет разбит на 2²ⁿподобных ему (с коэффициентом >2ⁿ) треугольничков, которые мы обозначим черезX_j,  1 ≤j≤ 2ⁿ  (рис. справа).  После отображенияhⁿкаждыйX_iперейдёт в некоторыйY_j, и если затем переставить числа в тройке  (α_n, β_n, γ_n)  в порядке убывания – применить  f_j, то произведение двух преобразований  f_j°hⁿотображаетX_iнаY₁(преобразование подобия с коэффициентом 2ⁿ).   Мы утверждаем, что в каждом из 2²ⁿтреугольниковX_i⊂Y₁  существует ровно одна такая "неподвижная точка"y_i, что  y_i∈X_i  и  f_j(hⁿ(y_i)) =y_i.  Из ответа нужно еще исключить неподвижные точки тех треугольниковX_i, у которых большие катеты лежат на большем катете треугольникаY₁(их существует именно столько, каков коэффициент подобия), поскольку для этих (и, как нетрудно видеть, только для этих) треугольников "неподвижная точка" попадает на границу, где отображениеhⁿне определено. Отсюда сразу следует, что ответ в нашей задаче:  2²ⁿ– 2ⁿ.  (На рис. справа в каждом из 12 голубых треугольничков лежит по одной точке  (α, β, γ),  для которой  (α_n, β_n, γ_n)  после перестановки в порядке убывания совпадает с (α, β, γ).)   Докажем наше утверждение. Для этого мы применим к треугольникуY₁и отображениюpэтого треугольника наX_i⊂Y₁,  обратному к  f_j°hⁿ, следующую теорему.  Теорема. ПустьZ– многоугольник (все граничные точкиZсчитаются принадлежащимиZ),  p:Z→Z  – преобразование подобия с коэффициентом  k< 1.  Тогда существует ровно одна "неподвижная точка" преобразованияp, принадлежащаяZ, то есть только одна точкаz₀∈Z,  для которой p(z₀) =z₀.  Доказательствоаналогично решению задачи158014.

а) либо  ^π/₄< α, β, γ <^π/₂,  либо два угла меньше^π/₄, а третий меньше^3π/₄. б) Когда один из углов α, β или γ равен^πs/_2ⁿ. г)  2²ⁿ– 2ⁿтреугольников.