Разберём сначала особый случай  a = 0.  Получаем: 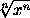  + 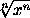= 0.

  Если n чётно, то единственным решением будет  x = 0  (иначе один из корней не имеет смысла). Если же n нечётно, то любое x будет решением.

  Пусть теперь  a ≠ 0.  Обозначив    через y, а a – y через z, получаем систему:  y + z = a,  yⁿ + zⁿ = aⁿ.

  Пусть  y = a,  z = 0  или  y = 0,  z = a.  В этих случаях оба равенства выполняются. Посмотрим, какие это даёт ответы. Вычислим  x:  xⁿ = 2aⁿ  или  xⁿ = aⁿ.

  Эти равенства выполняются при     и  x = a,  если n нечётно, и при 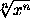    и  x = ± a,  если n чётно, (в этом случае  a ≥ 0).  Подставляя эти значения x в исходное уравнение, получаем в обоих случаях одно и то же:  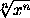 = a.

  Докажем теперь, что при  a ≠ 0  либо y, либо z равно нулю. Достаточно рассмотреть случай  a > 0, y ≥ z.  Действительно, если  (y, z, a)  – решение системы, то и  (– y, – z, – a)  – также её решение. Далее, если в решении поменять значения y и z местами, то получим снова решение. Рассмотрим два случая.

  а)  z > 0.  Но тогда равенство  yⁿ + zⁿ = (y + z)ⁿ  невозможно.

  б)  z = – w < 0.  При чётном n система принимает вид

    y – w = a,

    yⁿ + wⁿ = aⁿ.

  Решений нет: из первого уравнения  y > a,  откуда  yⁿ + wⁿ > yⁿ > aⁿ.

  При нечётном n система принимает вид

    y – w = a,

    yⁿ – wⁿ = aⁿ,

или

    a + w = y,

    aⁿ + wⁿ = yⁿ,

что аналогично случаю а).

Если n нечётно, то при  a ≠ 0   x₁ = a ,  x₂ = a;  при  a = 0   x – любое.

Если n чётно, то при  a > 0   x_1,2 = ± a ,  x_3,4 = ± a;  при a = 0   x = 0,  а при  a < 0  решений нет.