Приведем решение для общего случая, когда в каждой строчке не4, а n звездочек. Докажем, что при наилучшей игре противников разность окажется равной4 · 10^n-1.

а) Стратегия второго игрока.

Если первая цифра, названная первым игроком, 4 или меньше, второй игрок ставит ее вместо старшего разряда уменьшаемого. После этого, как только первый игрок назовет цифру, отличную от 0, второй заполняет ею старший разряд вычитаемого. Разность окажется не большей чем n- n<4 · 10^n-1. Если первый игрок, начиная со второго хода, каждый раз называет 0, то разность также будет меньше, или равна 4 · 10^n-1.

Если первый игрок начинает с цифр 5, 6, 7, 8 или 9, второй ставит ее на место старшего разряда вычитаемого, а затем занимает старший разряд уменьшаемого первой же названной цифрой, отличной от 9. Даже если все последующие цифры– девятки, то также получится разность, не превосходящая 4 · 10^n-1.

б) Стратегия первого игрока.

До тех пор пока остаются свободными старшие разряды уменьшаемого и вычитаемого, первый игрок называет цифры 4 и 5. Начиная с момента, когда второй игрок заполнит один из двух старших разрядов, и до конца игры первый игрок называет0, если раньше оказался заполненным старший разряд уменьшаемого, и 9– в противном случае. Остается уточнить, в каких случаях первый игрок называет цифру 4, а в каких– цифру5.

Перед очередным своим ходом первый игрок мысленно проставляет нули во всех незаполненных разрядах. Если после этого разность оказывается неотрицательной, он объявляет цифру 4, если же разность отрицательна– цифру5.

Докажем, что описанная стратегия первого игрока позволяет ему сделать разность не меньшей 4 · 10^n-1.

Если старший разряд вычитаемого займет цифра 4, то в старшем разряде уменьшаемого окажется цифра9:

Если старший разряд уменьшаемого заполнит цифра 5, то старший разряд вычитаемого займет цифра0,а

Предположим, что первый игрок назвал цифру 4, а второй заполнил ею старший разряд уменьшаемого. Перед этим ходом разность была неотрицательной, после хода она увеличилась на 4 · 10^n-1 и больше не изменялась, так как при всех следующих ходах первый игрок называл0.

Осталось рассмотреть случай, когда первый игрок назвал цифру 5, а второй заполнил ею старший разряд вычитаемого. Разобьем цифры, называемые первым игроком, на серии, объединяя в серию одинаковые цифры, идущие подряд. Будем считать, что второй игрок не ставит друг под другом одинаковые цифры, в противном случае их можно было бы перечеркнуть и не рассматривать при дальнейших рассуждениях. Докажем теперь, что каждая серия из четверок кончается так:

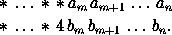
То, что первая серия кончается так, очевидно. Пусть s -ая серия из четверок кончается таким образом. Покажем, что и s+1-ая серия закончится так же. После s -ой серии четверок пойдет серия из пятерок. Рассмотрим самую левую пятерку из этой серии (напомним, что перечеркнутых цифр мы не рассматриваем!). Ясно, что она попадет в уменьшаемое в разряд с номером, меньшим m , а под ней стоит либо звездочка, либо, если она попала в m-1-ый разряд, четверка. Эта пятерка– последняя в своей серии. Действительно, после того, как она поставлена, разность становится положительной и первый начнет объявлять четверки. Если рассмотреть теперь самую левую четверку из s+1-ой серии, то, с помощью таких же рассуждений можно убедиться, что она стоит в вычитаемом в разряде, более близком к первому, чем последняя пятерка из предыдущей серии, над ней стоит звездочка и что она– последняя в своей серии.

Поэтому после того, как названа последняя четверка, возникнет следующая ситуация

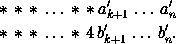
После этого первый игрок один или несколько раз назвал цифру 5 и, так как после каждого его хода уменьшаемое оставалось меньше вычитаемого (при мысленной замене звездочек нулями), то перед объявлением девяток возникло следующее положение

где для каждого i=2, 3, ..., k-1 либо a_i=a'_i , либо a'_i=5 и a_i – звездочка, причем разность чисел

отрицательна. Действительно, если бы она была положительна, то перед объявлением девяток первый игрок объявил бы четверку, а нулем она быть не может, поскольку a_k либо звездочка, либо пятерка. С другой стороны, ясно, что если при i<k a_i и a'_i – не звездочки, то a_i=a'_i ; действительно, они совпадали в момент объявления последней четверки. Поэтому для некоторого j k a_j – звездочка, а под ней стоит четверка или пятерка. Но тогда ясно, что окончательная разность не меньше 4 · 10^n-1+3 · 10^n-j>4 · 10^n-1. Задача решена.

Ответ задачи отсутствует