Задача
С натуральным числом (записываемым в десятичной системе) разрешено проделывать следующие операции:А) приписать на конце
Решение
a) Вместо того чтобы получить с помощью операций А, Б, В из числа4число1972, мы попробуем получить из числа1972число4с помощью обратных операций:
А' ) вычеркивание цифры 4 в конце;
Б' ) вычеркивание цифры 0 в конце;
В' ) умножение числа на 2.
При этом мы будем каждый раз, как только это возможно, применять операцию А' или Б' , чтобы по возможности на каждом шаге уменьшать наше число. Получим:
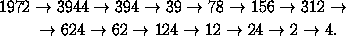
Ясно, что прочитав эту последовательность от конца к началу, мы получим нужный результат. (Операция Б' здесь не используется.)
б) Докажем, что если с каждым числом N поступать так же, как мы поступали с числом 1972 (применять операцию А' или Б' , а если это не возможно– В' ), то через несколько шагов мы придем к числу4.
Для этого достаточно доказать, что в получающейся мри этом последовательности каждое число через несколько шагов превратится в меньшее число (или в число 4). Отсюда будет следовать, что в конце концов мы обязательно придем к числу 4, поскольку нельзя построить бесконечной последовательности натуральных чисел, в которой за каждым числом встречается меньшее.
Итак, убедимся, что каждое число за несколько операций А' , Б' , В' можно уменьшить (или прийти из него к 4; этот последний случай мы дальше особо не оговариваем).
Если последняя цифра числа 0 или 4, то после применения А' или Б' оно уменьшается по крайней мере в 10 раз.
Пусть последняя цифра числа отлична от 0 и 4. В табл.1 показано, как меняется последняя цифра при применении В' (операция В' , т.е. увеличение числа в 2 раза, обозначена черной стрелкой, возможность применения А' или Б' – красной стрелкой):
Таблица1
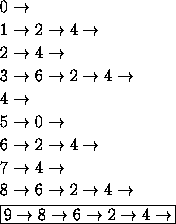
Из этой таблицы видно, что если число N оканчивается на любую цифру,
кроме 9, то после не более чем трехкратного применения В' , т.е.
после увеличения не более, чем в 8 раз, к нему можно применить А'
или Б' , т.е. уменьшить его по крайней мере в 10 раз. В итоге из
N получится число, не превосходящее  N<N .
N<N .
Осталось рассмотреть лишь числа N , заканчивающиеся на 9, которые до перехода к А' увеличиваются в 16 раз. Заметим, что какой бы ни была предыдущая перед 9 цифра числа N , предпоследняя цифра числа
Если эта цифра не 8, то 16N после А' и не более чем двух операций В' превратится снова в число с цифрой 0 или 4 на конце, которое мы можем уменьшить по крайней мере в 10 раз. В итоге из А' получится число, не превосходящее
 <N.
<N.
Остался случай, когда 16N оканчивается на 84. Заметим, что какой бы ни была предыдущая перед 8 цифра этого числа, после операций
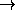 10b+8
10b+8 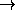
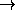
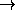 80b+64
80b+64 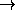 8b+6
8b+6Если эта цифра не 8, то не более чем за две операции В мы получаем число
с цифрой 0 или 4 на конце, отбрасываем ее и в итоге получаем из N
число, не превосходящее 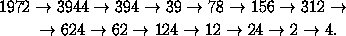 N<N . Если же эта
цифра– 8, то за три операции В' мы получаем число с четной
предпоследней цифрой и из него (после А' , не более чем трехкратного
применения В' и откидывания последней цифры)– число, не превосходящее
N<N . Если же эта
цифра– 8, то за три операции В' мы получаем число с четной
предпоследней цифрой и из него (после А' , не более чем трехкратного
применения В' и откидывания последней цифры)– число, не превосходящее
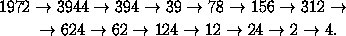 N=
N=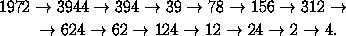 N<N.
N<N.
Наше утверждение доказано, и задача решена.
Попробуйте, разобравшись в этом решении, перевести с помощью операций А, Б, В число 4 в 1249 (это одно из самых "неприятных" чисел).
Многие читатели, которые решали задачу M140 этим путем, не заметили или не до конца разобрали случай, когда число N оканчивается на9.
Значительно более короткое решение придумали А.Асташов (Львов), А.Арсасян (Камо), Г.Высоцкая (Красноярск). Они доказывают, что из любого четного числа можно с помощью операций А' , Б' , В' получить меньшее четное число (ясно, что этого достаточно для решения задачи). Здесь достаточно рассмотреть 5 случаев:
-
10k
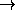 k ,
k , -
10k+2
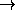 20k+4
20k+4 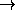 2k ,
2k , -
10k+4
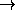 k
k 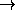 2k ,
2k , -
10k+6
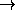 20k+10+2
20k+10+2 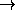 40k+20+4
40k+20+4 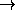 4k+2,
4k+2, -
10k+8
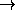 20k+10+6
20k+10+6 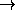 40k+30+2
40k+30+2 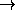 80k+60+4
80k+60+4 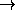 8k+6.
8k+6.
Ниже мы публикуем список читателей, приславших нам правильные решения некоторых из задач M129-M140. По поводу задач M129, M130, M137, M140, условие которых состояло из нескольких пунктов, мы получили очень много писем с ответами на самые простые вопросы, но в список включены только те, кто решил задачи а) и б). (Впрочем, задачу M130б не решил никто.)
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь