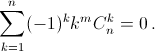
Решение 1:   Рассмотрим алфавит из n букв  {a₁, a₁, ..., a_n}.  Подсчитаем двумя способами количество слов длины m. С одной стороны, оно равно n^m. С другой стороны, такие слова не могут содержать все буквы алфавита (так как  m < n),  поэтому все такие слова принадлежат объединению

A₁ ∪ ... ∪ A_n ,   где A_i  – множество всех слов длины m, не содержащих букву a_i. Заметим, что пересечение k множеств типа A_i  – это множество слов, записанных в алфавите из  n – k  букв, поэтому оно состоит из  (n – k)^m  слов. Теперь по формуле включения-исключения получаем

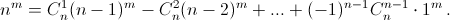    Это эквивалентно доказываемому равенству.

Решение 2:   Рассмотрим многочлены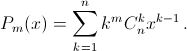   

  Заметим, что   P₁(x) = ((1 + x)ⁿ)′,   P_m+1(x) = (xP_m(x))′.   Поскольку число  –1  является корнем многочлена  (1 + x)ⁿ  кратности n, то оно будет корнем многочлена P₁(x) кратности  n – 1,  корнем P₂(x) кратности  n – 2,  ..., корнем P_m(x) кратности  n – m.  А интересующая нас сумма равна  P_m(–1).

Ответ задачи отсутствует