Задача
Пустьa,b,c,
Решение
Поскольку для любого невыпуклого четырехугольника легко построить выпуклый
четырехугольник со сторонами той же длины и имеющий большую площадь (рис. 1),
то ясно, что достаточно доказать неравенства а), б) для выпуклого
четырехугольника. Поэтому мы будем рассматривать только выпуклые
четырехугольники.
Итак, пусть в выпуклом четырехугольнике ABCD (рис. 2) AB=a , BC=b , CD=c , DA=d , площадь ABCD равна5. Площадь треугольника всегда не превышает
половины произведения двух его сторон (рис. 3). Поэтому
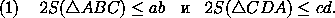 Сложив эти неравенства, получим
Сложив эти неравенства, получим
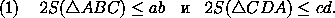 Равенство здесь достигается в том случае, когда оно достигается
одновременно в обоих неравенствах (1), т. е. в том и только в том случае,
когда углы B и D — оба прямые. Разумеется, в этом случае
четырехугольник ABCD можно вписать в окружность (причем диагональ AC является диаметром). Из сказанного выше следует также, что четырехугольник,
для которого2S=ab+cd , можно составить из отрезков a , b , c , d в том и только в том случае, если их длины удовлетворяют условию
Равенство здесь достигается в том случае, когда оно достигается
одновременно в обоих неравенствах (1), т. е. в том и только в том случае,
когда углы B и D — оба прямые. Разумеется, в этом случае
четырехугольник ABCD можно вписать в окружность (причем диагональ AC является диаметром). Из сказанного выше следует также, что четырехугольник,
для которого2S=ab+cd , можно составить из отрезков a , b , c , d в том и только в том случае, если их длины удовлетворяют условию
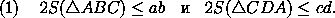 Задача б) несколько труднее. Ее можно решить "в лоб", применяя различные
формулы для площадей треугольников. Но есть и совсем простое геометрическое
решение.
Разрежем четырехугольник, как и раньше, диагональю BD на два треугольника
и один из них — скажем, треугольник BCD — "перевернем на обратную
сторону" и снова приложим стороной BD к треугольнику BAD . Другими
словами, заменим Δ BCD треугольником BC'D , симметричным
ему относительно перпендикуляра, проходящего через середину отрезка BD (рис. 4). Ясно, что площадь четырехугольника S от этого не изменится.
Но теперь мы можем воспользоваться результатом задачи а):
Задача б) несколько труднее. Ее можно решить "в лоб", применяя различные
формулы для площадей треугольников. Но есть и совсем простое геометрическое
решение.
Разрежем четырехугольник, как и раньше, диагональю BD на два треугольника
и один из них — скажем, треугольник BCD — "перевернем на обратную
сторону" и снова приложим стороной BD к треугольнику BAD . Другими
словами, заменим Δ BCD треугольником BC'D , симметричным
ему относительно перпендикуляра, проходящего через середину отрезка BD (рис. 4). Ясно, что площадь четырехугольника S от этого не изменится.
Но теперь мы можем воспользоваться результатом задачи а):
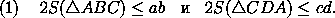 AB · BC'+C'D · DA
AB · BC'+C'D · DA
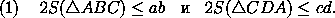 Рис. 137.3. SΔ ABC=hb/2
Рис. 137.3. SΔ ABC=hb/2 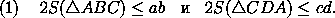 ab/2.
Равенство в (4) достигается, если у "перестроенного" четырехугольника ABC'D углы B и D — прямые, т. е. если у исходного четырехугольника ABCD углы, которые диагональ BD образует с каждой парой противоположных
сторон, в сумме дают по90o :
ab/2.
Равенство в (4) достигается, если у "перестроенного" четырехугольника ABC'D углы B и D — прямые, т. е. если у исходного четырехугольника ABCD углы, которые диагональ BD образует с каждой парой противоположных
сторон, в сумме дают по90o :
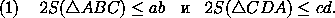 Отсюда конечно, следует, что
Отсюда конечно, следует, что 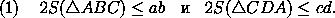 ABC+
ABC+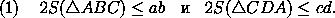 ABC=180o , т. е.
четырехугольник ABCD — вписанный (это ясно и из того, что
ABC=180o , т. е.
четырехугольник ABCD — вписанный (это ясно и из того, что 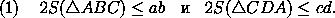 A+
A+
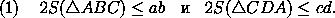 C=
C=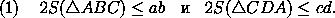 A+
A+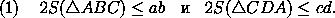 C'=180o ). (Заметим, что четырехугольник,
для которого
C'=180o ). (Заметим, что четырехугольник,
для которого
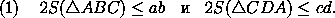 можно составить из отрезков a , b , c , d в том и только в том случае,
когда
можно составить из отрезков a , b , c , d в том и только в том случае,
когда
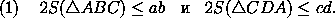 это следует из (3) в применении к ABC'D .)
Еще одно замечание. Не кажется ли вам странным, что необходимое и достаточное
для равенства (6) условие (5) "несимметрично"?
Ведь в (6) обе пары противоположных вершин участвуют равноправно —
чем же диагональ BD лучше, чем AC ? Она, конечно, ничем не лучше. Мы
сейчас увидим, что условие (5) можно заменить симметричным и
поэтому, как часто бывает, более простым.
Легко проверить (рис. 5), что условие (5) эквивалентно просто
такому: четырехугольник ABCD — вписанный и AC
это следует из (3) в применении к ABC'D .)
Еще одно замечание. Не кажется ли вам странным, что необходимое и достаточное
для равенства (6) условие (5) "несимметрично"?
Ведь в (6) обе пары противоположных вершин участвуют равноправно —
чем же диагональ BD лучше, чем AC ? Она, конечно, ничем не лучше. Мы
сейчас увидим, что условие (5) можно заменить симметричным и
поэтому, как часто бывает, более простым.
Легко проверить (рис. 5), что условие (5) эквивалентно просто
такому: четырехугольник ABCD — вписанный и AC 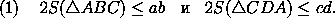 BD .
Теперь мы можем сформулировать наш результат так: для того, чтобы
выполнялась равенство (6), необходимо и достаточно, чтобы
четырехугольник ABCD был вписанным и имел взаимно перпендикулярные
диагонали.
(Попутно мы еще доказали, что для таких четырехугольников выполняется
условие (7). Вспомните, как это сделать!).
Кроме решения с "переворачиванием треугольника" еще одно простое решение
задачи б) основано на неравенстве Птолемея, т. е. на такой теореме
(см. "Квант" # 4, 1972, стр. 45, решение M99):
В любом четырехугольнике ABCD
BD .
Теперь мы можем сформулировать наш результат так: для того, чтобы
выполнялась равенство (6), необходимо и достаточно, чтобы
четырехугольник ABCD был вписанным и имел взаимно перпендикулярные
диагонали.
(Попутно мы еще доказали, что для таких четырехугольников выполняется
условие (7). Вспомните, как это сделать!).
Кроме решения с "переворачиванием треугольника" еще одно простое решение
задачи б) основано на неравенстве Птолемея, т. е. на такой теореме
(см. "Квант" # 4, 1972, стр. 45, решение M99):
В любом четырехугольнике ABCD
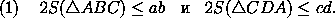 причем равенство здесь достигается тогда и только тогда, когда
четырехугольник ABCD — вписанный.
Из этой теоремы следует, что ( ϕ — угол между диагоналями)
причем равенство здесь достигается тогда и только тогда, когда
четырехугольник ABCD — вписанный.
Из этой теоремы следует, что ( ϕ — угол между диагоналями)
S=AC · BD · sin ϕ 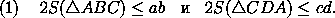 AB · CD+AD · BC=ac+bd.
AB · CD+AD · BC=ac+bd.
На этом пути условия равенства сразу получаются в "симметричном" виде (но зато труднее получить условие (7)).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь