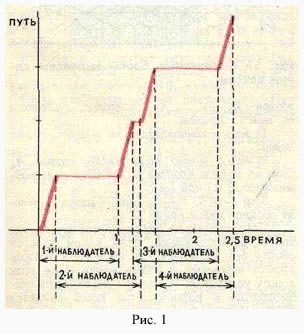
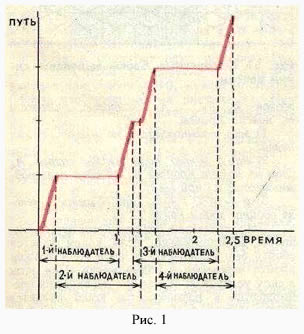
На рис. 1 изображен график, показывающий, что за 2,5 минуты улитка может проползти 4 м.

  Легко видеть, что аналогично можно так расположить наблюдателей и так задать движение улитки, что заtминут (t> 1) она проползёт  2(t– 1) м,  еслиt– целое, и 2[t], еслиt– не целое.   Докажем, что это – максимальное перемещение улитки.   Пустьa₁– первый наблюдатель. Рассмотрим всех наблюдателей, которые начали следить за улиткой либо в тот момент, когда кончилa₁, либо ещё раньше (по условию такие наблюдатели есть). Пустьa₂– последний из таких наблюдателей. Рассмотрим, далее, всех наблюдателей, начавших следить за улиткой не позже, чем кончилa₂, и обозначим черезa₃последнего из них. Аналогично выберем наблюдателяa₄и т.д. Очевидно, что в конце концов мы дойдём до наблюдателя, окончившего наблюдать как раз в конце последней минуты (если наблюдательa_kкончил наблюдать раньше, то имеются наблюдатели, начавшие следить позже, чем началa_k, а потому можно выбрать наблюдателяa_k+1).   Пусть  a₁,a₂, ...,a_k  – все выбранные таким образом наблюдатели. Ясно, что промежутки наблюдения  a₁,a₃,a₅, ...  не пересекаются; точно так же не пересекаются промежутки, в которых следили наблюдатели  a₂,a₄,a₆, ...   Действительно, если бы, например, нашёлся момент времени, когда наблюдалиa₁иa₃, то это означало бы, что наблюдательa₂выбран неправильно, так какa₃начал наблюдать позже, чем началa₂, но ещё до того, как кончилa₁.   Так как промежутки наблюдения  a₁,a₃,a₅, ...  не пересекаются, то этих наблюдателей заtминут меньшеt. Поэтому еслиt– целое, их не больше t– 1,  а еслиtне целое, то не больше [t]. Тем же числом ограничивается количество наблюдателей "чётной группы":  a₂,a₄,a₆, ...   Так как выделенное множество наблюдателей покрывает весь интервал наблюдения, то улитка не могла проползти больше суммы перемещений, зафиксированных всеми наблюдателями, то есть больше  2(t– 1),  еслиt– целое, и 2[t] – если не целое).   Оценим теперь число "нечётных" наблюдателей снизу. Если все зазоры между соседними нечётными наблюдателями меньше единицы, то число нечётных наблюдателей должно быть больше [^t/₂]. Это означает, что улитка не могла проползти путь, меньший  [^t/₂] + 1.  На рис.2 показано, как должна двигаться улитка, чтобы этот минимум был достигнут.

[^t/₂] + 1  метр;  2(t – 1)  метров, если t – целое,  2[t]  метров, если t – не целое.