Задачи и олимпиады по математике

Задача

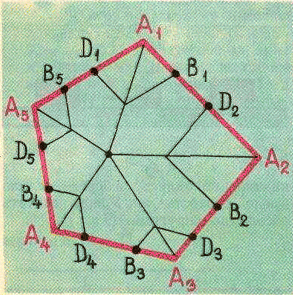
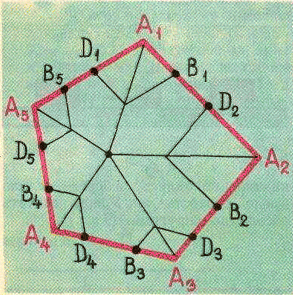
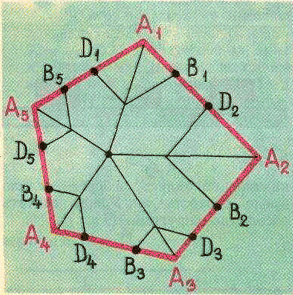
а) Дан выпуклый многоугольник A₁A₂...A_n. На стороне A₁A₂ взяты точки B₁ и D₂, на стороне A₂A₃ – точки B₂ и D₃, ..., на стороне A_nA₁ – точки B_n и D₁ так, что если построить параллелограммы A₁B₁C₁D₁, A₂B₂C₂D₂, ..., A_nB_nC_nD_n, то прямые A₁C₁, A₂C₂, ..., A_nC_n пересекутся в одной точке. Докажите равенство A₁B₁·A₂B₂·...·A_nB_n = A₁D₁·A₂D₂·...·A_nD_n.

б) Докажите, что для треугольника верно и обратное утверждение: если на сторонеA₁A₂выбраны точкиB₁иD₂, на сторонеA₂A₃– точкиB₂иD₃, а на сторонеA₃A₁– точкиB₃иD₁так, что A₁B₁·A₂B₂·A₃B₃=A₁D₁·A₂D₂·A₃D₃, то, построив параллелограммыA₁B₁C₁D₁,A₂B₂C₂D₂иA₃B₃C₃D₃, получим прямыеA₁C₁,A₂C₂иA₃C₃, пересекающиеся в одной точке.

Решение

а) Пусть O – точка пересечения. Запишем равенство, которое нам нужно доказать, так: 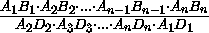= 1.

Теперь заметим, что отношения отрезков 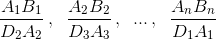соответственно равны отношениям площадей треугольников 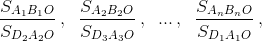так что нужное нам равенство можно записать так: 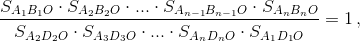или

Но последнее равенство очевидно. Действительно, площади треугольников A_iB_iO и A_iD_iO для каждого i = 1, 2, ..., n равны, поскольку они имеют общую сторону A_iO и равные высоты (рис. слева); высоты, опущенные из вершин B_i и D_i на сторону A_iO, равны, потому что диагональ A_iC_i делит параллелограмм A_iB_iC_iD_i на два равных треугольника.

б) Обратную теорему можно вывести из прямой. ПустьP– точка пересечения прямыхA₁C₁иA₂C₂. Предположим, что прямаяA₃Pне проходит через точкуC₃. Тогда она пересекает одну из сторонB₃C₃илиD₃C₃параллелограммаA₃B₃D₃C₃, скажем,D₃C₃(рис. справа) в точкеC'₃. Выберем на сторонеA₃A₁такую точкуB'₃, чтоA₃B'₃C'₃D₃– параллелограмм. Теперь согласно п. а) A₁B₁·A₂B₂·A₃B'₃=A₁D₁·A₂D₂·A₃D₃, с другой стороны, по условию A₁B₁·A₂B₂·A₃B₃=A₁D₁·A₂D₂·A₃D₃, поэтому A₃B'₃=A₃B₃, следовательно, наше предположение о том, что точкиC₃иC'₃(и, следовательно, точкиB₃иB'₃) не совпадают, неверно.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления