Задачи и олимпиады по математике

Задачи Подборки Авторы

Задача 173625 • Сложность: 3 • 9-11 класс

Задача

Еслиx₁ < x₂ < x₃ < ... < x_n —натуральные числа, то суммаn – 1дробей,k-я изкоторых, гдеk < n,равна отношению квадратного корня из разностиx_k+1 - x_kк числуx_k+1, меньше суммы чисел 1,¹/₂,¹/₃, ...,¹/_n². Докажите это.

Решение

Предположим сначала, что x_n≤n². Тогда

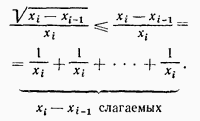
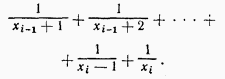
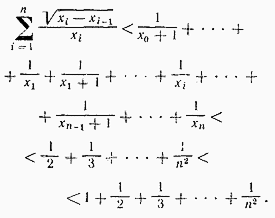
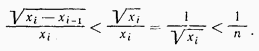
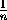Последняя сумма, очевидно, не превосходит содержащей столько же слагаемых суммы

Но тогда

Предположим теперь, что среди чисел x₀, x₁, x₂, ..., x_n есть большие, чем n². Если x_i > n², то Таким образом, каждое слагаемое со знаменателем x_i, большим n² , меньше . Следовательно, сумма всех таких слагаемых (их не более чем n ) меньше1. Но сумма остальных слагаемых, как уже было показано выше, меньше 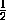+ + 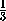... + 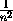, что и завершает доказательство исходного неравенства.