Эту задачу можно сформулировать еще следующим образом. Пусть p_i – отображение, которое каждой точке M (на плоскости) ставит в соответствие ее проекцию на прямую l_i , т.е. p_i(M)– основание перпендикуляра, опущенного из точки M на прямую l_i . Требуется доказать, что на прямой l₁ существует единственная точка X₁ такая, которая после n отображений

X₁ p_n X_n p_n-1 X_n-1p_n-2 ...p₂ X₂ p₁ X₁

переходит в себя.

Для произвольной точки X прямой l₁ обозначим через f(X)ту точку на прямой l₁ , в которую переходит X после n отображений p_n , p_n-1, ... , p₁ (рис.1); это записывается так:

f=p₁ o p₂ o ...o p_n.

Выберем на каждой из наших прямых l_i начало отсчета и направление, т.е. превратим каждую из них в числовую ось (единицу масштаба мы выбираем на всех прямых одинаковой). (Мы отождествляем точку (на прямой) и соответствующее ей число– ее координату– так, что отображения p₁, p₂, ...p_n и f можем считать теперь функциями, которые каждому числу ставят в соответствие новое число.) Ниже дана подпись к рис.1

Рис.1. Отображение f: x 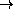f(x)называется произведением отображений p₄, p₃, p₂, p₁ .

Ответ задачи отсутствует