Докажем, что для каждого натурального k существует ровно одно натуральное n такое, что 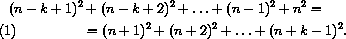(Заметьте, что в правой части равенства стоит(k-1)слагаемое, а в левой– k ). Равенство(1) эквивалентно следующим: 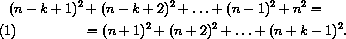Таким образом, высказанное утверждение доказано: равенство(1) для натуральных k и n выполняется тогда и только тогда, когда n=2k²-2k . (При переходе от(3) к(4) мы воспользовались тем, что сумма(k-1)членов арифметической прогрессии(2n-k+2)+(2n-k+4)+...(2n+k-2)равна(k-1) ((2n-k+2)(2n+k-2))/2=2(k-1)n .) Тем самым мы получили искомую общую формулу. Ее можно записать, например, так: 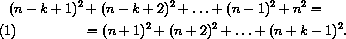где k – произвольное натуральное число. Примеры, приведенные в условия, получаются из нее при k , равном2, 4и5.

Ответ задачи отсутствует