Задача
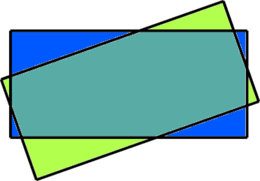 Два одинаковых прямоугольника расположены так, что их контуры пересекаются в восьми точках. Докажите, что площадь пересечения этих прямоугольников больше половины площади каждого из них.
Два одинаковых прямоугольника расположены так, что их контуры пересекаются в восьми точках. Докажите, что площадь пересечения этих прямоугольников больше половины площади каждого из них.
Решение
Пусть длины сторон прямоугольников a и b . Заметим, что на сторонах
каждого из прямоугольников лежит ровно две точки пересечения с двумя
соседними сторонами другого. (Легко доказать, что если всего точек
пересечения8, то на каждой стороне должно лежать не меньше двух точек
и что пересечение стороны одного прямоугольника с двумя параллельными
сторонами другого невозможно). Пусть A и C — точки, в которых
пересекаются стороны разных прямоугольников, равные a ; B и D —
точки, в которых пересекаются стороны, равные b . Тогда, очевидно, отрезок AC служит биссектрисой угла между сторонами длины a , проходящими через
точку A (для доказательства достаточно опустить на эти стороны
перпендикуляры из точки C и рассмотреть пару образовавшихся при этом
равных треугольников). Точно так же BD — биссектриса угла между
сторонами длины b , проходящими через точку B . Следовательно, AC  BD , и поэтому площадь выпуклого четырехугольника с диагоналями AC и BD равна
BD , и поэтому площадь выпуклого четырехугольника с диагоналями AC и BD равна  . Поскольку AC
. Поскольку AC  b и BD
b и BD  a , даже
эта площадь (и уж подавно вся площадь общей части прямоугольников)
больше
a , даже
эта площадь (и уж подавно вся площадь общей части прямоугольников)
больше 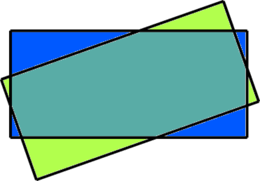 .
Как показывают письма читателей, самое трудное в подобной задаче —
придумать безупречное рассуждение, которое годилось бы для всех возможных
случаев расположения фигур, не зависело бы от особенностей чертежа.
Поэтому мы намеренно не ссылались в решении на рисунок, чтобы подчеркнуть,
что правильность решения можно проверить формально, не обращаясь ни
к какому конкретному рисунку.
.
Как показывают письма читателей, самое трудное в подобной задаче —
придумать безупречное рассуждение, которое годилось бы для всех возможных
случаев расположения фигур, не зависело бы от особенностей чертежа.
Поэтому мы намеренно не ссылались в решении на рисунок, чтобы подчеркнуть,
что правильность решения можно проверить формально, не обращаясь ни
к какому конкретному рисунку.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь