Предположим, что в некотором прямоугольнике со сторонами a и b  (a < b)  сумма по модулю равна  4 + ε,  где  ε > 0.  Построим четыре квадрата, у каждого из которых три стороны идут по некоторым трём сторонам этого прямоугольника a×b; тогда прямые, на которых лежат четвёртые стороны этих квадратов, образуют новый прямоугольник со сторонами  2b – a  и  |2a – b|  (см. рис. 1 и 2; случай  b = 2a,  разумеется, невозможен).

  Докажем, что в этом новом прямоугольнике сумма чисел по модулю не меньше  4 + 3ε.   Можно считать, что  s₄+s₅+s₆= 4 + ε  (если эта сумма равна  – (4 + ε),  то заменим знаки у всех чисел на противоположные).   Рассмотрим сначала случай  b< 2a.  Тогда    s₅= (s₄+s₅) + (s₅+s₆) – (s₄+s₅+s₆) ≤ 1 + 1 – 4 – ε = –2 – ε,    s₂+s₈= (s₁+s₂+s₃+s₄+s₅+s₆) + (s₄+s₅+s₆+s₇+s₈+s₉) –s₁–s₃–s₇–s₉– 2(s₄+s₅+s₆) ≤ 1 + 1 + 1 + 1 + 1 + 1 – 2(4 + ε) = –2 – 2ε, откуда  s₂+s₅+s₈≤ –4 – 3ε.   Аналогично если  b> 2a,  то    s₅= –s₄–s₅+ (s₄+s₅+s₆) ≤ –1 – 1 + 4 + ε ≤ 2 + ε,    s₂+s₈= (s₁+s₂) + (s₂+s₃) + (s₇+s₈) + (s₈+s₉) – (s₁+s₂+s₃+s₄+s₅+s₆) – (s₄+s₅+s₆+s₇+s₈+s₉) + 2(s₄+s₅+s₆) ≥ 2 + 2ε,    s₂+s₅+s₈≥ 4 + 3ε.   Итак, мы доказали, что если в прямоугольнике  a₁×b₁  сумма чисел по модулю больше  4 + ε,  то в новом прямоугольнике  a₂×b₂,  где a₂= |2a₁–b₁|, b₂= 2b₁–a₁,  сумма чисел по модулю больше  4 + 3ε.  Для прямоугольникаa₂×b₂  мы можем построить точно тем же способом новый прямоугольник  a₃×b₃,  в котором сумма чисел будет больше  4 + 3·3ε = 4 + 9ε,  и так далее – такую последовательность прямоугольников  a₁×b₁, a₂×b₂,  ..., a_n×b_n,  ...,  что в прямоугольнике  a_n×b_n  сумма чисел по модулю больше  4 + 3^n–1ε.   Докажем, что в этой последовательности все прямоугольники, начиная с некоторого, будут относиться ко второму типу, то есть для них b_n> 2a_n.  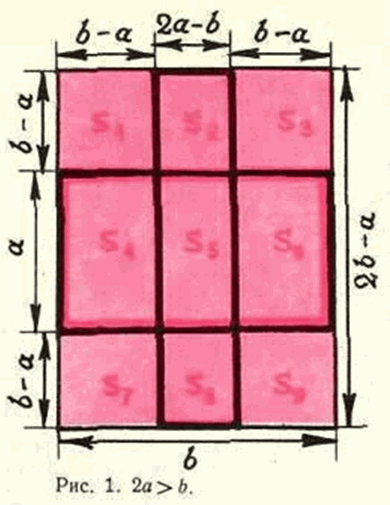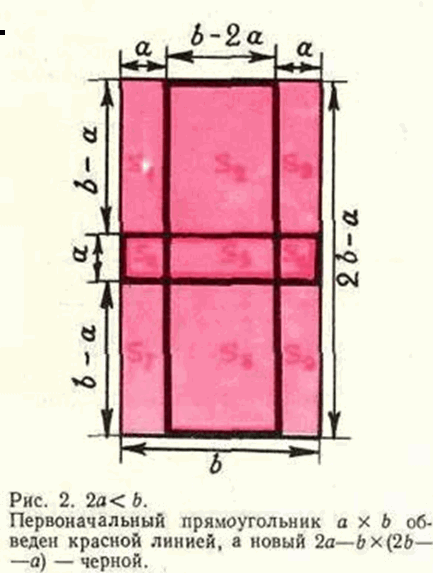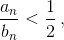Действительно, во-первых, легко проверить, что если    то и 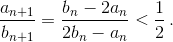   Во-вторых, если  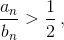  то 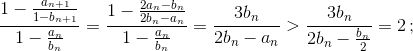   таким образом, величина  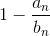  при переходе отnк  n+ 1  увеличивается не менее чем в два раза до тех пор, пока мы не придём к прямоугольнику с  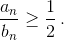  Поэтому, каким бы малым ни было  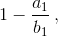  всегда после нескольких операций мы придём к прямоугольнику второго типа, и дальше в нашей последовательности будут встречаться только такие прямоугольники.   Поэтому можно считать, что уже 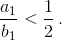    При этом  a₃=b₂– 2a₂= (2b₁–a₁) – 2(b₁– 2a₁) = 3a₁, b₃= 2b₂–a₂= 2(2b₁–a₁) – (b₁– 2a₁) = 3b₁.   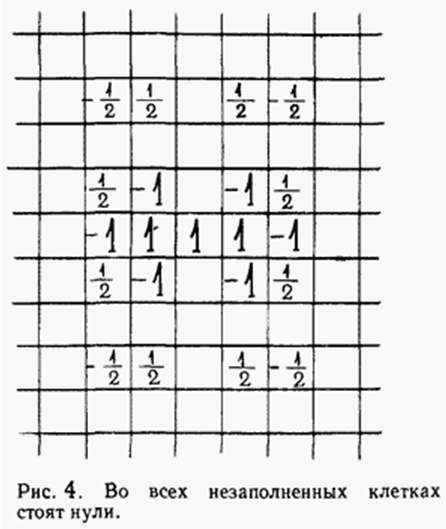Следовательно, вообще  a_2k+1= 3^ka₁  и  b_2k+1= 3^kb₁,  причём сумма чисел в этом прямоугольнике  3^ka₁×3^kb₁  больше  4 + 9^kε,  то есть, выбравkдостаточно большим, мы можем сделать её сколь угодно большой. Но прямоугольник  Na₁×Nb₁,  гдеa₁,b₁иN– целые числа, можно разбить наa₁b₁квадратов (со сторонойN), и поэтому сумма чисел в нём не может превосходить по модулю числаa₁b₁. Противоречие.   Рис. 3 поясняет вторую половину доказательства.   г) На рис.4 изображен пример, для которого сумма чисел в некотором прямоугольнике равна 3. Таким образом, для  c < 3  утверждение задачи неверно.   в) Решение этой задачи неизвестно. Более того, весьма правдоподобно, что точная оценка  c = 4.  Впрочем, примеры, показывающие, что c может быть больше 3, тоже неизвестны.

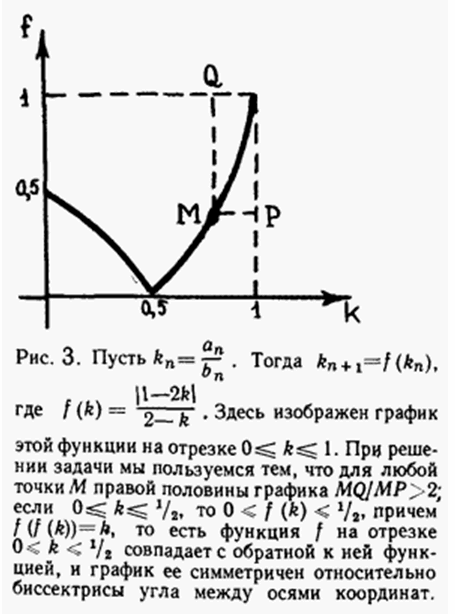
Ответ задачи отсутствует