Заметим сначала, что если мы будем переставлять между собой строки (или столбцы) нашей таблицы, то это не повлияет ни на условие задачи, ни на то, что нам требуется доказать. Предположим, что перестановками строк и столбцов мы собрали в правый верхний угол размером k×m одни нули (см. рис.).

  Подсчитаем сумму чисел, стоящих в куске, обозначенном на рисунке буквой C. Сумма чисел, стоящих в куске B, равна m (m столбцов, в каждом из которых сумма равна 1). Аналогично, сумма чисел в куске A равна k (k строк). Так как сумма всех чисел в таблице равна n, то на долю куска C остаётся  n – m – k.  Это число неотрицательно, так как по условию в таблице все числа неотрицательны. Итак,  n – m – k ≥ 0,  то есть  m + k ≤ n.

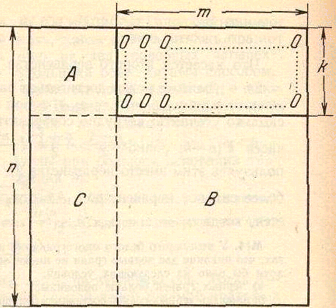
  Теперь мы можем переформулировать задачу так: в таблице n×n стоят числа, и известно, что никакой перестановкой строк и столбцов нельзя выделить в ней такой угол из нулей размером k×m, что  m + k > n;  доказать, что можно выбрать n отличных от нуля чисел, никакие два из которых не стоят ни в одном столбце, ни в одной строке. (Для нас теперь не важно, что числа положительны и что суммы по строкам и столбцам равны 1. В дальнейшем мы различаем только "нули" и "не нули".)

  Новая формулировка задачи есть просто запись на языке "таблиц" теоремы о сватовстве (см. решение задачи 198160). Действительно, запишем в строки таблицы n×n юношей, а в столбцы – девушек (пусть и тех и других по n). На пересечении i-й строки и j-го столбца поставим "не-нуль" (звездочку), если i-й юноша знаком с j-й девушкой, и 0, если незнаком. Получим таблицу (матрицу) знакомств. (см. рис.).

  Возьмём произвольную группу из k юношей. Поставим соответствующие им строки первыми. Если с какой-то девушкой ни один из этих юношей не знаком, то в соответствующем столбце в первых k строках стоят нули. Если все столбцы, соответствующие таким девушкам, мы переставим последними (пусть их число равно m), то мы получим угол из нулей размером k×m.

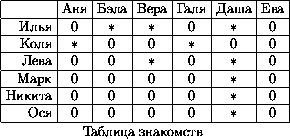
  В каждом из первых  n – m  столбцов есть хотя бы один "не-нуль" в первых строках, так как соответствующая девушка имеет друзей из числа выбранных нами k юношей. Так как  m + k ≤ n,  то  n – m ≥ k,  то есть таких девушек не меньше k.

Ответ задачи отсутствует