Задача
 |
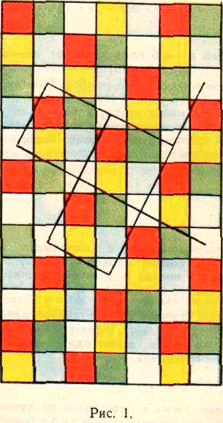а) На рис. 1 плоскость покрыта квадратами пяти цветов. Центры квадратов одного и того же цвета расположены в вершинах сетки из одинаковых квадратов. При каком числе n цветов возможно аналогичное заполнение плоскости? б) На рис. 2 плоскость покрыта шестиугольниками семи цветов так, что центры шестиугольников одного и того же цвета образуют вершины решётки из одинаковых правильных треугольников. При каком числе n цветов возможно аналогичное построение? Примечание. Имеются в виду только такие заполнения плоскости фигурками (квадратами или шестиугольниками), при котором сетка, соответствующая какому-то одному цвету, имеет такие же размеры и направления сторон квадратов (или треугольников), как и сетка, соответствующая любому другому цвету (то есть все сетки должны получаться друг из друга параллельным сдвигом). |  |
Решение
Мы рассмотрим оба случая сразу.
Примем за единицу длины расстояние между центрами двух соседних фигурок (квадратов или шестиугольников).
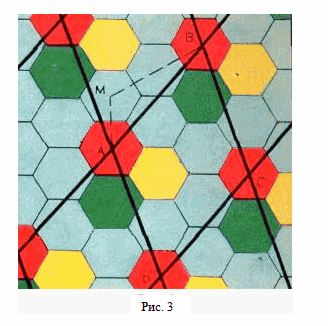
Начертим сетку, проходящую через центры фигурок одного цвета, скажем, красного. В случае шестиугольников мы проведём линии только двух направлений, так что сетка будет состоять не из правильных треугольников, а из ромбов (рис. 3).
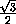(k² +kl + l²).
Число цветов, участвующих в раскраске, равно отношению
площадиABCDк площади одной окрашенной фигурки, а именно:
в случае квадратов k² +l²,
в случае шестиугольников k² +kl + l².
Это сразу следует из следующей леммы. Лемма. Часть ABCD, закрашенная каждым цветом, участвующим в раскраске, либо представляет собой одну фигурку, либо состоит из кусочков (для красного цвета – четырёх, для других цветов – двух), из которых можно сложить такую же фигурку.
Доказательство леммы несложно. Теперь пусть нам дано число m = k² + l² или n = k² + kl + l². Покажем, что плоскость можно заполнить в соответствии с условием квадратами m цветов или шестиугольниками n цветов.
Заполним плоскость фигурками и начнём их раскрашивать следующим образом. Закрасим одну из них красным. Отсчитаем от неё k фигурок в одну сторону, потом повернем на 90° для квадратов и на 60° для шестиугольников, отсчитаем l фигурок в новом направлении и ту фигурку, в которую мы придём, тоже закрасим красным. На отрезке, соединяющем центры двух красных фигурок, как на стороне построим квадрат (а) или правильный треугольник (б). Пристраивая к нему равные квадраты (правильные треугольники), мы получим центры всех фигурок, которые надо закрасить красным; сдвигая параллельно всю совокупность красных фигурок, мы будем получать каждый раз новую совокупность незакрашенных фигурок и закрашивать её новым цветом, пока не закрасим всю плоскость.
По доказанному выше число цветов будет равно k² + l² в случае а) и k² + kl + l² в случае б).
Ответ
а) При n = k² + l², б) при n = k² + kl + l², где k, l – целые неотрицательные числа (но не равные нулю одновременно).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь