Задача
На стороне $CD$ прямоугольника $ABCD$ взята точка $K$. Из вершины $B$ опустили перпендикуляр $BH$ на отрезок $AK$.
Оказалось, что отрезки $AK$ и $BH$ делят прямоугольник на три части, в каждую из которых можно вписать круг (см. рисунок).
Докажите, что если круги, касающиеся стороны $CD$, равны, то и третий круг им равен.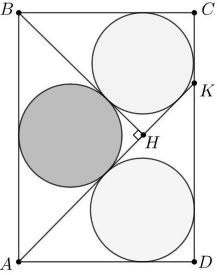
Решение
Уточним, что точки $H$ и $K$ предполагаются различными, как на рисунке (иначе утверждение задачи неверно).
Продлим отрезок $AK$ до пересечения с прямой $BC$ в точке $E$. Два правых круга симметричны относительно горизонтальной средней линии нашего прямоугольника. Значит, углы $CBH$ и $DAH$ равны, то есть $AHB$ — равнобедренный прямоугольный треугольник. Поэтому и $BHE$ — равнобедренный прямоугольный треугольник, равный треугольнику $AHB$. А окружности, вписанные в равные треугольники, равны.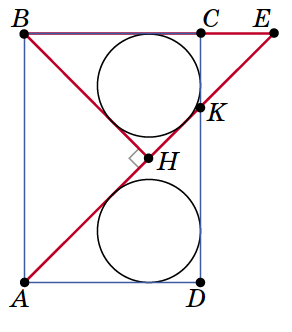
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь