Пусть $M$, $N$ и $K$ – середины рёбер одинаковой длины $AA_1$, $A_1C_1$ и $BC$. Построим сечение нашей призмы плоскостью. Для этого проведём прямую $MN$ до пересечения с продолжениями рёбер $AC$ и $CC_1$ в точках $P$ и $Q$, а затем проведём прямые $KP$ и $KQ$ (см. рисунок). Получим пятиугольное сечение $MNRKS$.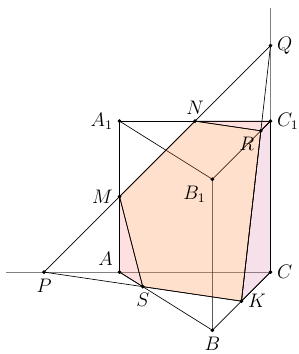Чтобы узнать отношение объёмов, вычислим сначала объём одной из частей как разности треугольной пирамиды $CQPK$ и треугольных пирамид $QNRC_1$ и $PMAS$. Из условия следует, что две боковые грани призмы $AA_1C_1C$ и $BB_1C_1C$ – квадраты. Пусть их стороны равны $4a$, тогда $$PA = NC_1 = QC_1 = CK = 2a.$$ Треугольники $RQC_1$ и $KQC$ подобны с коэффициентом $\frac{QC_1}{QC} = \frac13$, поэтому $RC_1=\frac23 , a$. Если в треугольнике $ABC$ провести среднюю линию через $KL$ параллельно $AB$, получим $AS= \frac12 , KL=\frac14 , AB$.

Объём треугольной пирамиды $CQPK$ равен $$V = \frac16 \cdot CQ \cdot CP \cdot CK = \frac16 \cdot 6a \cdot 6a \cdot 2a = 12a^3;$$ объём пирамиды $PMAS,$ вершины $M$, $A$ и $S$ которой расположены на рёбрах того же трёхгранного угла с вершиной $P$, равен $$V \cdot \frac{PS}{PK} \cdot \frac{PA}{PC} \cdot \frac{PM}{PQ} = V \cdot \frac12 \cdot \frac13 \cdot \frac 13 = \frac23 , a^3;$$ объём пирамиды $QNRC_1$ равен $$\frac16 \cdot C_1Q \cdot C_1N \cdot C_1R = \frac16 \cdot 2a \cdot 2a \cdot \frac23 , a = \frac49 , a^3.$$

Итак, одна из двух частей, на которые плоскость $PQK$ делит призму, имеет объём $$12 a^3 - \frac23 , a^3 - \frac49 , a^3 = \frac{98}9 , a^3.$$ Объём всей призмы равен $\frac12 , 4a \cdot 4a \cdot 4a = 32a^3$, поэтому объём оставшейся части равен $$32a^3 - \frac{98}{9} , a^3 = \frac{190}{9} , a^3.$$ Таким образом, отношение объёмов меньшей части к большей равно $\frac{98}{190} = \frac{49}{95}$.

$\frac{49}{95}$.