Задача
Из прямого угла прямоугольного треугольника опущена высота, и в образовавшиеся треугольники вписаны два квадрата (как на рисунке).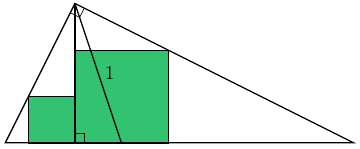 Чему может быть равна сумма площадей этих квадратов, если длина биссектрисы прямого угла треугольника равна $1$?
Чему может быть равна сумма площадей этих квадратов, если длина биссектрисы прямого угла треугольника равна $1$?
Решение
Решение 1:Опустим из основания биссектрисы перпендикуляры на стороны большого треугольника и обозначим вершины, как на рисунке.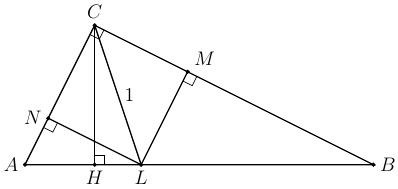 Поскольку $CL$ – биссектриса, $LN = LM$, а так как угол $C$ прямой, то треугольники $CML$ и $CNL$ – прямоугольные равнобедренные, то есть $CMLN$ – квадрат.
Опустим теперь перпендикуляры из точек $N$ и $M$ на $AB$ и $CH$. Закрашенные на рисунке ниже треугольники равны по гипотенузе (стороне квадрата $CMLN$) и острому углу, так как
$$\angle NCQ = 90^\circ - \angle SCM = \angle CMS = 90^\circ - \angle SML = \angle LMR = 180^\circ - 90^\circ - \angle MLR =\angle NLP.$$
Поскольку $CL$ – биссектриса, $LN = LM$, а так как угол $C$ прямой, то треугольники $CML$ и $CNL$ – прямоугольные равнобедренные, то есть $CMLN$ – квадрат.
Опустим теперь перпендикуляры из точек $N$ и $M$ на $AB$ и $CH$. Закрашенные на рисунке ниже треугольники равны по гипотенузе (стороне квадрата $CMLN$) и острому углу, так как
$$\angle NCQ = 90^\circ - \angle SCM = \angle CMS = 90^\circ - \angle SML = \angle LMR = 180^\circ - 90^\circ - \angle MLR =\angle NLP.$$
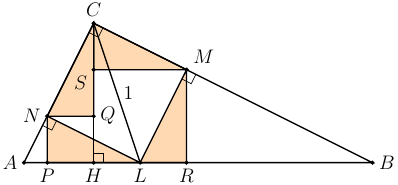 Это, в частности, означает, что $NQHP$ и $SMRH$ – квадраты, причём это в точности вписанные в треугольники $ACH$ и $BCH$ из условия задачи!
Остаётся заметить, что их суммарная площадь равна $NP^2 + HR^2 = NP^2+PL^2 = NL^2$, а $NL$ – сторона квадрата с диагональю 1. Значит, $NP^2 + HR^2 = NL^2 = \left(\frac{1}{\sqrt{2}}\right)^2 = \frac12.$
Это, в частности, означает, что $NQHP$ и $SMRH$ – квадраты, причём это в точности вписанные в треугольники $ACH$ и $BCH$ из условия задачи!
Остаётся заметить, что их суммарная площадь равна $NP^2 + HR^2 = NP^2+PL^2 = NL^2$, а $NL$ – сторона квадрата с диагональю 1. Значит, $NP^2 + HR^2 = NL^2 = \left(\frac{1}{\sqrt{2}}\right)^2 = \frac12.$
Решение 2:Опустим из основания биссектрисы перпендикуляры на стороны большого треугольника и обозначим вершины, как на рисунке.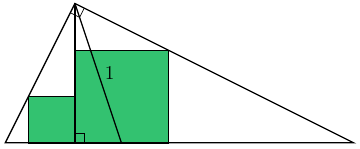 Поскольку $CL$ – биссектриса прямого угла, то $CMNL$ – квадрат. Пусть $S$ – площадь этого квадрата. Прямоугольные треугольники $ACH$, $CBH$ и $ABC$ подобны по двум углам. Площади квадратов, вписанных в прямые углы этих треугольников, относятся, как квадраты коэффициентов подобия. Значит, сумма площадей двух меньших квадратов равна
$$S \cdot \left(\frac{AC}{AB}\right)^2 + S \cdot \left(\frac{BC}{AB}\right)^2 = S \cdot \frac{\left(AC^2 + BC^2\right)}{AB^2} = S.$$
Диагональ квадрата площади $S$ – это биссектриса $CL$, и она равна $1$. Значит, сторона большого квадрата равна $\frac{1}{\sqrt{2}}$, а его площадь $S = \left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2}$. Поэтому сумма площадей двух меньших квадратов тоже равна $\frac{1}{2}$ и не зависит от углов исходного треугольника.
Поскольку $CL$ – биссектриса прямого угла, то $CMNL$ – квадрат. Пусть $S$ – площадь этого квадрата. Прямоугольные треугольники $ACH$, $CBH$ и $ABC$ подобны по двум углам. Площади квадратов, вписанных в прямые углы этих треугольников, относятся, как квадраты коэффициентов подобия. Значит, сумма площадей двух меньших квадратов равна
$$S \cdot \left(\frac{AC}{AB}\right)^2 + S \cdot \left(\frac{BC}{AB}\right)^2 = S \cdot \frac{\left(AC^2 + BC^2\right)}{AB^2} = S.$$
Диагональ квадрата площади $S$ – это биссектриса $CL$, и она равна $1$. Значит, сторона большого квадрата равна $\frac{1}{\sqrt{2}}$, а его площадь $S = \left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2}$. Поэтому сумма площадей двух меньших квадратов тоже равна $\frac{1}{2}$ и не зависит от углов исходного треугольника.
Ответ
$\frac{1}{2}$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь