Распилим мысленно каждый брусок на два кубика и будем выкладывать куб из них. У нас получилось $108$ красных и $108$ белых кубиков. У каждого кубика на поверхности большого куба может оказаться от нуля до трёх граней-клеточек. Три грани на поверхности будут у восьми угловых кубиков. Две грани – у кубиков, расположенных вдоль рёбер большого куба, но не на углу. Вдоль каждого из $12$ ребер таких кубиков $4$, а всего их $48$. Больше всего красных клеточек окажется на поверхности, если красными будут эти $8 + 48 = 56$ кубиков, а также $108 - 56 = 52$ кубика с одной гранью на поверхности. Тогда на поверхности окажется $3 \cdot 8 + 2 \cdot 48 + 52 = 172$ красных клеточки. Приведём теперь пример выкладывания брусков, приводящего к такому результату. Из $28$ красных брусков сложим каркас (см. рисунок), а из $32$ белых брусков – внутренний куб $4 \times 4 \times 4$. 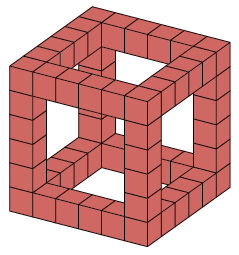Оставшиеся шесть квадратных «окон» $4\times4$ на каждой грани заполним произвольно. Тогда на поверхности куба будет $120$ красных клеток каркаса (по $20$ на каждой грани) и ещё $52$ красных клетки (по две у каждого из оставшихся $54 - 28 = 26$ красных брусков). Итого $120 + 52 = 172$ клетки.