Решение 1:Пусть $ABCD$ – данный квадрат.1-2. Дважды согнув квадрат по прямым, параллельным $AD$, построим на сторонах $AB$, $CD$ точки $U$, $V$ соответственно такие, что $AU=DV=1/4$.

3-7. Согнув квадрат пять раз по прямым, параллельным $AB$, разделим сторону $AD$ и отрезок $UV$ на 32 равных части.

8. Согнув квадрат по прямой $ST$, где $S$ – точка на $AD$ такая, что $SD=23/32$, а $T$ – точка на $UV$ такая, что $TV=1/32$, получим на $CD$ точку $P$ такую, что $PV:PD=1:23$, т.е. $PV=1/88$.

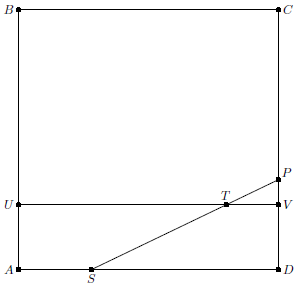9. Аналогично согнув квадрат по прямой $S'T$, где $DS'=24/32$, получим на $CD$ такую точку $Q$, что $VQ=1/92$. Соответственно $PQ=1/2024$.

Решение 2:Обозначим через $X_n$ такую точку на стороне $AD$, что $DX_n=AD/n$, а через $Y_n$ такую точку на диагонали $BD$, что $DY_n=BD/n$.Лемма. Для любого $n$ прямая $X_nY_{n+1}$ проходит через $C$.

Для доказательства достаточно применить теорему Менелая к треугольнику $AOD$, где $O$ – центр квадрата, и точкам $X_n$, $Y_{n+1}$, $C$.

Пользуясь леммой, проведем следующее построение.

1. Перегнем квадрат по диагонали $BD$.

2. Перегнув квадрат по средней линии, отметим точку $X_2$.

3. Перегнув квадрат по прямой $CX_2$, отметим $Y_3$.

4-5. Разделив отрезок $DY_3$ на четыре части, отметим точку $Y_{12}$.

6. Перегнув квадрат по прямой $CY_{12}$, отметим точку $X_{11}$.

7. Разделив отрезок $DX_{11}$ пополам, отметим точку $X_{22}$.

8. Перегнув квадрат по прямой $CX_{22}$, отметим точку $Y_{23}$.

9. Перегнув квадрат по прямой, проходящей через $Y_{23}$ и параллельной $CD$, отметим точку $X_{23}$.

10-11. Разделив отрезок $X_{22}X_{23}$ на четыре части, получим отрезок длины $(1/22-1/23)/4=1/2024$.

Ответ задачи отсутствует