Задача
Биссектрисы $AA_1$, $CC_1$ треугольника $ABC$, в котором $\angle B=60^{\circ}$, пересекаются в точке $I$. Описанные окружности треугольников $ABC$, $A_1IC_1$ пересекаются в точке $P$. Докажите, что прямая $PI$ проходит через середину стороны $AC$.
Решение
Так как $\angle A_1IC_1=120^{\circ}=180^{\circ}-\angle A_1BC_1$, окружности $ABC$ и $A_1IC_1$ пересекаются в точках $B$ и $P$. Поэтому треугольники $PA_1C$ и $PC_1A$ подобны, т.е. $PB_1:PC_1=A_1C:AC_1$. С другой стороны, поскольку $\angle AC_1I+\angle IA_1C=180^{\circ}$, то, применяя теорему синусов к треугольникам $AC_1I$ и $CA_1I$, получаем, что $A_1C:AC_1=IC:IA$. Следовательно, $\sin\angle PIA_1:\sin\angle PIC_1=IC:IA$ и $IP$ – медиана треугольника $IAC$.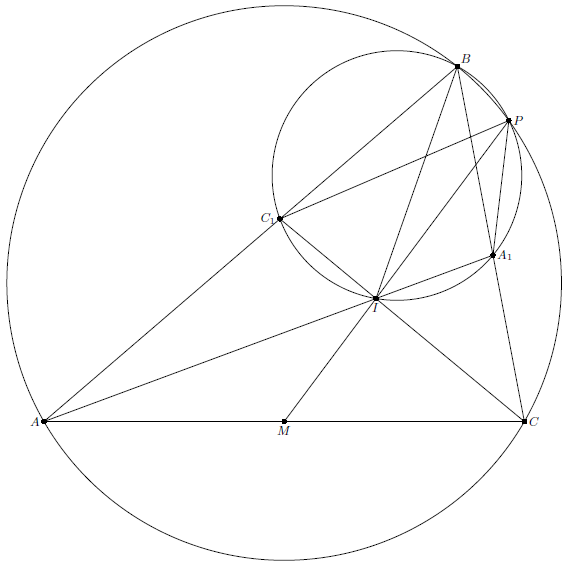
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь