Задача
Биссектрисы $AI$ и $CI$ пересекают описанную окружность треугольника $ABC$ в точках $A_1$, $C_1$ соответственно. Описанная окружность треугольника $AIC_1$ пересекает сторону $AB$ в точке $C_0$; аналогично определим $A_0$. Докажите, что точки $A_0,$ $A_1$, $C_0$, $C_1$ лежат на одной прямой.
Решение
Пусть прямая $A_1C_1$ пересекает $AB$ в точке $A'$. Тогда
$$
\angle C_1A'A=(\smile AC_1+\smile BA_1)/2=(\smile AC_1+\smile A_1C)/2=\angle C_1IA.
$$
Следовательно, точки $A$, $I$, $A'$, $C_1$ лежат на одной окружности и $A'$ совпадает с $A_0$. Аналогично получаем, что $A_1C_1$ проходит через $C_0$.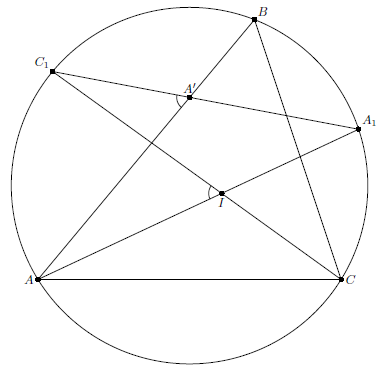
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет