Проведём через пару скрещивающихся рёбер тетраэдра $ABCD$ две параллельные плоскости. Так же поступим для двух других пар скрещивающихся рёбер и получим параллелепипед. Диагонали его граней равны между собой, поэтому все грани  – прямоугольники, и параллелепипед прямоугольный. Пусть $O$  – его центр, являющийся также центром описанной сферы тетраэдра $ABCD$. 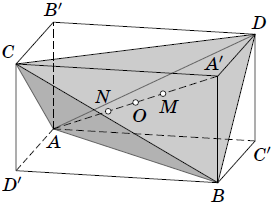Пусть также $A'$, $B'$, $C'$, $D'$  – точки, симметричные $A$, $B$, $C$, $D$ соответственно относительно точки $O$ (см. рисунок). Докажем, что все построенные прямые проходят через точку $O$.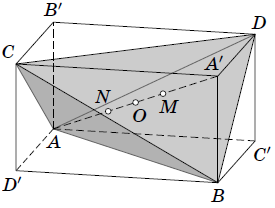Пусть $M$  – центр масс треугольника $BCD$. Тогда $$\overrightarrow{A'M}=\frac13\cdot(\overrightarrow{A'B}+\overrightarrow{A'C}+\overrightarrow{A'D})=\frac13\cdot \overrightarrow{A'A},$$ то есть точка $M$ лежит на диагонали $AA'$ и делит её в отношении $2: 1$, считая от вершины $A$. Аналогично центр масс $N$ треугольника $B'C'D'$ лежит на этой диагонали и делит её в отношении $1: 2$, считая от вершины $A$. Точка $O$  – середина отрезка $NM$, поэтому $AO:OM=3: 1$. Рассмотрим проекцию на плоскость $BCD$: $A''$  – проекция точки $A$, $O_A$  – проекция центра $O$. Точка $O$ совпадает с центром описанной сферы тетраэдра $ABCD$, поэтому $O_A$  – центр описанной окружности треугольника $BCD$.

Тогда прямая $AA'$ проецируется в прямую Эйлера $O_AM$ треугольника $BCD$. Пусть $O_AM = x$. Тогда $O_A A'' = 3x$ ($O$ делит отрезок $AM$ в отношении $3:1$, это отношение сохраняется при проецировании). Кроме того, $O_A$, $M$, $H_A$ лежат на одной прямой и $O_AM : MH_A =1: 2$ (прямая Эйлера), отсюда $MH_A=2x$. Следовательно, $O_AA'' = O_AH_A$, т. е. точка $O_A$ является проекцией середины отрезка $AH_A$ на плоскость $BCD$. Прямая $OO_A$, перпендикулярная плоскости $BCD$, делит отрезок $AH_A$ пополам, а значит, совпадает с прямой $h_A$. Итак, все построенные прямые проходят через точку $O$.

Ответ задачи отсутствует