Рассмотрим 12-угольник $A_1A_2\ldots A_{12}$, удовлетворяющий условию задачи. У него десять сторон длины 1 и одна сторона длины 2. Обозначим через $x$ длину оставшейся стороны. Рассмотрим векторы $\overrightarrow{A_1A_2}$, $\overrightarrow{A_2A_3}, \ldots, \overrightarrow{A_{12}A_1}$, а также коллинеарные им единичные векторы $\vec{e}_1$, $\vec{e}2, \ldots, \vec{e}{12}$. Тогда для некоторых $i$ и $j$ имеет место равенство $$\vec{e}_1 +\ldots +2\vec{e}_i +\ldots +x\vec{e}j +\ldots +\vec{e}{12} =\vec{0}.$$ Помимо того, $$\vec{e}_1 +\vec{e}_7 =\vec{e}_2 +\vec{e}_8 =\ldots =\vec{e}6 +\vec{e}{12} =\vec{0},$$ поэтому $$\vec{e}_1 +\vec{e}2 +\ldots +\vec{e}{12} =\vec{0}.$$ Вычитая второе из полученных равенств из первого, получаем $\vec{e}_i +(x-1)\vec{e}j = \vec{0}$. Это возможно лишь в случае, если $\vec{e}i =-\vec{e}j$ и $x =2$. Значит, в исходном 12-угольнике есть пара параллельных сторон длины 2.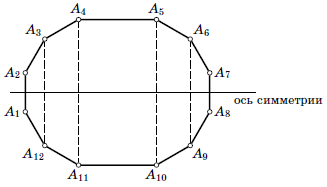 В силу равенства всех углов и соответствующих сторон этот 12-угольник имеет ось симметрии (см. рисунок). Чтобы найти площадь, разобьём его на 4 трапеции и прямоугольник. Находим $A_3A{12}=A_6A_9=1+\sqrt{3}$, $A_4A{11}=A_5A{10} =2+\sqrt{3}$, поэтому искомая площадь равна $$S=2\cdot(2+\sqrt{3})+\frac{\sqrt{3}\cdot(2+\sqrt{3}+1+\sqrt{3})}{2}+\frac{1+\sqrt{3}+1}{2}=8+4\sqrt{3}.$$

$8+4\sqrt{3}$.