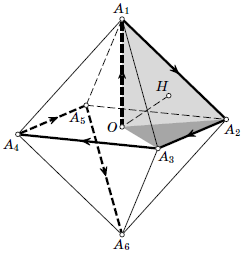
Пусть корабль находится в некоторой точке $O$. Рассмотрим правильный октаэдр $A_1A_2A_3A_4A_5A_6$, описанный возле шара радиуса $a$ с центром в точке $O$. Докажем, что путь $O\rightarrow A_1\rightarrow A_2 \rightarrow A_3 \rightarrow A_4 \rightarrow A_5 \rightarrow A_6$ заведомо позволит достигнуть граничной плоскости. Предположим противное. Но тогда вершины октаэдра, а значит, и сам октаэдр (выпуклая оболочка его вершин) лежат строго внутри полупространства. Поэтому вписанный шар октаэдра, радиус которого равен $a$, тоже лежит строго внутри полупространства. Получаем противоречие, так как по условию расстояние до граничной плоскости полупространства равно $a$.

Покажем теперь, что длина пути $O\rightarrow A_1\rightarrow A_2 \rightarrow A_3 \rightarrow A_4 \rightarrow A_5 \rightarrow A_6$ меньше $14a$. Пусть $OA_1=OA_2=OA_3=x$, $OH$ – высота пирамиды $OA_1A_2A_3$. Запишем ее объём двумя способами: $$V=\frac16 x^3=\frac13\cdot OH\cdot S_{A_1A_2A_3} = \frac 13 \cdot a\cdot\sqrt3\cdot\frac{(x\sqrt2)^2}4.$$ Отсюда получаем, что $x=a\sqrt3$, а длина ребра октаэдра равна $a\sqrt6$. Поэтому длина пути равна $(\sqrt3+5\sqrt6)a < 14a$, так как $\sqrt2 < 43/30$.

Ответ задачи отсутствует