Отметим на планете полюсы $N$ и $S$, и пусть точки $A$, $B$, $C$ и $D$ делят соответствующий экватор на четыре равных дуги, как на рисунке ниже. 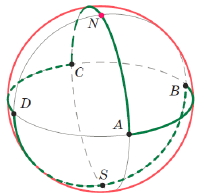Рассмотрим замкнутый путь $A\rightarrow B\rightarrow S\rightarrow D\rightarrow C\rightarrow N\rightarrow A$ по поверхности, состоящий из дуг больших окружностей с центрами в центре планеты. Этот путь состоит из 6 одинаковых дуг длиной в 1/4 экватора, поэтому длина пути составляет 600 км.

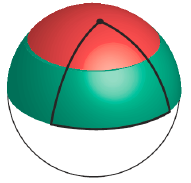
Покажем, что луноход побывал на расстоянии не более 50 км от каждой точки. Поверхность планеты разобьём на 8 одинаковых сферических треугольников с вершинами в отмеченных точках. Луноход побывал во всех вершинах и во всех точках хотя бы одной стороны каждого треугольника. Так как расстояние по поверхности от полюса до экватора 100 км, то поверхность планеты разбивается на экваториальный пояс – точки, удалённые от экватора на расстояние не более 50 км, – и две полярные шапки – точки, удалённые от полюсов на расстояние не более 50 км. На рисунке ниже зелёная часть треугольника исследована луноходом, так как он проехал вдоль стороны, а красная исследована, так как он побывал в вершине.

Может.