Задача
Окружность, проходящая через вершину $B$ прямого угла и середину гипотенузы прямоугольного треугольника $ABC$, пересекает катеты этого треугольника в точках $M$ и $N$. Оказалось, что $AC = 2MN$. Докажите, что $M$ и $N$ — середины катетов треугольника $ABC$.
Решение
Пусть точка $M$ лежит на $AB$, точка $N$ – на $BC$, а точка $K$ – середина $AC$. Тогда $BK = 0,5AC$ (в прямоугольном треугольнике медиана равна половине гипотенузы). Так как угол $B$ прямой, то $MN$ – диаметр данной окружности. Поскольку $BK = 0,5AC = MN$, то $BK$ – тоже диаметр. Следовательно, $KM \perp AB$, то есть $KM$ – средняя линия треугольника $ABC$. Аналогично $KN$ – средняя линия.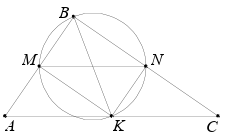
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет