Задача
В прямоугольном треугольнике $ABC$ ($\angle C=90^{\circ}$) вписанная окружность касается катета $BC$ в точке $K$. Докажите, что хорда вписанной окружности, высекаемая прямой $AK$ в два раза больше, чем расстояние от вершины $C$ до этой прямой.
Решение
Пусть $I$ – центр вписанной окружности, $P$, $Q$ – проекции точек $I$, $C$ соответственно на $AK$ (см. рис.).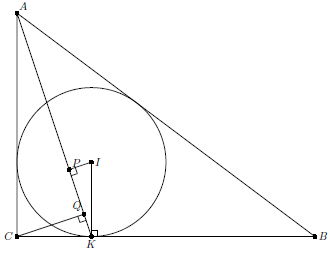 
Так как $\angle IKC=90^{\circ}$, $\angle ICK=45^{\circ}$, треугольник $IKC$ – равнобедренный, т.е. $IK=KC$. Кроме того, $\angle IKP=\angle KCQ$, поскольку соответствующие стороны этих углов перпендикулярны. Следовательно, треугольники $IKP$ и $KCQ$ равны, т.е. $KP=CQ$. Но $P$ – середина хорды, высекаемой в окружности прямой $AK$, откуда и следует утверждение задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь