Первое решение. Пусть исходные числа равняются $a_1$, $a_2$, $\ldots$, $a_n$. Докажем, что наибольшее из них, $A$, подходит (это достаточно естественный выбор: ведь если бы даже наибольшее число было меньше суммы квадратов всех чисел, то и все числа были бы меньше).

Для каждого $k$ выполняется неравенство $a_k^2\leqslant a_kA$. Складывая все такие неравенства, получаем $$ a_1^2+a_2^2+\ldots+a_n^2\leqslant a_1A+a_2A+\ldots+a_nA=(a_1+a_2+\ldots+a_n)A=A, $$ где последнее равенство следует из того, что сумма всех чисел равна 1. Второе решение. На рисунке ниже — геометрическое объяснение того же неравенства: квадраты со сторонами $a_i$ расположены внутри прямоугольника $A\times1$ (а значит, сумма площадей первых не превосходит площади последнего).

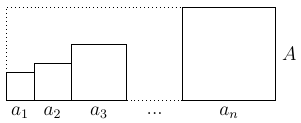
Ответ задачи отсутствует