Задача
На графике функции $y=1/x$ Миша отмечал подряд все точки с абсциссами 1, 2, 3, ..., пока не устал. Потом пришла Маша и закрасила все прямоугольники, одна из вершин которых — это отмеченная точка, еще одна — начало координат, а еще две лежат на осях (на рисунке показано, какой прямоугольник Маша закрасила бы для отмеченной точки $P$). Затем учительница попросила ребят посчитать площадь фигуры, состоящей из всех точек, закрашенных ровно один раз. Сколько получилось?
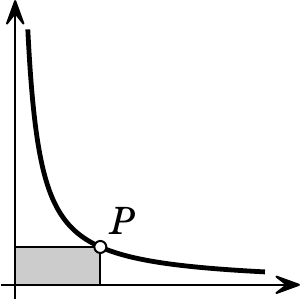
Решение
Пусть Миша устал, отметив точку с абсциссой $n$. Посмотрим, как устроена фигура, состоящая из всех точек, закрашенных ровно один раз. На отрезке абсцисс $[i-1, i]$, где $i=1,\ldots,n-1$, это прямоугольник ширины $1$ с высотой $h_i=\frac{1}{i} - \frac{1}{i+1}$. На отрезке $[n-1; n]$ это прямоугольник ширины $1$ с высотой $h_n = \frac{1}{n}$.
Тогда площадь фигуры
$ S = 1 \cdot h_1 + 1 \cdot h_2 + \ldots + 1 \cdot h_n =\left(1 - \frac12\right) + \left(\frac12 - \frac13\right) + \ldots + \left(\frac1{n-1} - \frac1n\right) + \frac1n = 1.$ Комментарии.
-
Можно провести рассуждение по индукции. Пусть Маша красит прямоугольник сразу, как только Миша отметил точку. Когда Миша отметит точку $(1;1)$, Маша закрасит прямоугольник площади $1$. Далее, когда Миша отмечает точку с абсциссой $n$, Маша закрашивает прямоугольник площади $\frac{1}{n}$ первый раз и площади $\frac{1}{n}$ — второй раз (остальное придётся на точки, уже закрашенные более одного раза). Таким образом, площадь фигуры, состоящей из всех точек, закрашенных ровно один раз, не изменяется.
-
Наглядно этот факт можно увидеть, «сдвинув» все прямоугольники к оси ординат.
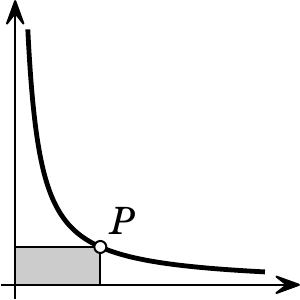
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь