Пусть A₀, B₀, C₀ – точки касания окружности ω со сторонами BC, CA, AB. Тогда искомые точки A', B', C' таковы, что четырёхугольники A'A₀C'C₀, B'B₀A'A₀ и C'C₀B'B₀ – гармонические (определение см. в замечании к задаче 165800). Действительно, из подобия треугольников BA'C₀ и BC₀C'; следует, что  A'C₀ : C₀C' = BA' : BC₀.  Аналогично  A'A₀ : A₀C' = BA' : BC₀,  поэтому  C₀A'·A₀C' = A'A₀·C'C₀,  то есть четырёхугольник A'A₀C'C₀ – гармонический.

  Сделаем проективное преобразование, сохраняющее ω и переводящее точку пересечения прямых AA₀, BB₀ и CC₀ в её центр (см. задачу 158424). Оно переведёт треугольник ABC в правильный. Тогда треугольники A₀B₀C₀ и A'B'C' тоже будут правильными, а четырёхугольник A'A₀C'C₀ будет равнобедренной трапецией. Пусть K – середина A₀C₀. Условие гармоничности  ∠C₀A'C' = ∠KA'A₀  (см. ссылки в задаче 165879) означает теперь, что  ∠KA'A₀ = ∠A₀C₀A' = ∠BA₀A',  откуда  A'K || BC || B₀C₀  (см. рис.).

  Теперь, сделав обратное преобразование, получаем следующее построение.   1-2. Проведём прямыеA₀C₀,BB₀и найдём точку их пересеченияK.   3-4. Проведём прямыеBCиB₀C₀и найдём точку их пересеченияL.   5. Проведём прямуюKLи найдём точкуA'её пересечения с дугойA₀C₀.   6. Проведём прямуюCA'и найдём точкуB'её пересечения с ω.   7. Проведём прямуюAB'и найдём точкуC'её пересечения с ω.

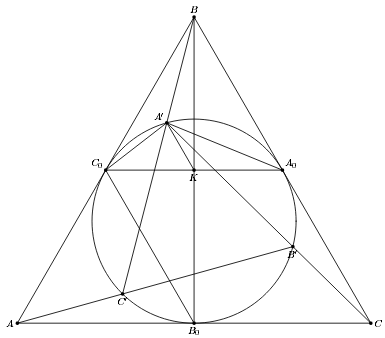
Ответ задачи отсутствует