Задача
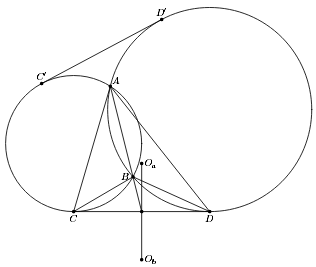
Две окружности пересекаются в точках A и B. Пусть CD – их общая касательная (C и D – точки касания), а Oa, Ob – центры описанных окружностей треугольников CAD, CBD соответственно. Докажите, что середина отрезка OaOb лежит на прямой AB.
Решение
Пусть C′, D′ – точки касания окружностей с второй общей касательной. Углы ACD и ADC равны половинам дуг AC и AD соответствующих окружностей, а углы BCD и BDC – половинам дуг BC и BD, которые равны дугам C′A и D′A (см. рис.). Следовательно, сумма всех четырёх углов равна полусумме дуг C′AC и D′AD. Поскольку последняя дуга гомотетична дуге C′C, эта полусумма равна 180°. Значит, центры описанных окружностей треугольников CAD и CBD симметричны относительно CD, то есть середина отрезка OaOb совпадает с серединой CD, которая лежит на прямой AB (см. задачу 152779).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь