Задача
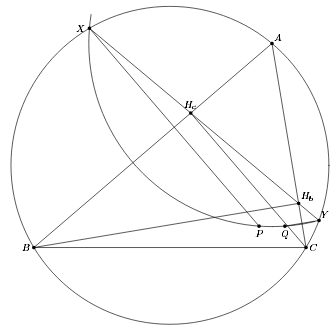
Пусть BHb, CHc – высоты треугольника ABC. Прямая HbHc пересекает описанную окружность Ω треугольника ABC в точках X и Y. Точки P и Q симметричны X и Y относительно AB и AC соответственно. Докажите, что PQ || BC.
Решение
Пусть O – центр Ω. Так как прямая AO симметрична высоте AHa относительно биссектрисы угла A (см. задачу 152358), а ∠AHbHc = ∠B, то
AO ⊥ HbHc, то есть AO – серединный перпендикуляр к отрезку XY. Следовательно, AP = AX = AY = AQ, то есть точки P, X, Y, Q лежат на окружности с центром A (см. рис.). Поэтому прямые XY и PQ антипараллельны относительно прямых XP и YQ, которые параллельны высотам треугольника. Но BC и HbHc также антипараллельны относительно высот, значит, PQ || BC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь