Пусть BB′, CC′ – высоты треугольника. Так как  ∠PHQ = 180° – ∠A = ∠B′HC′,  треугольники HB′Q и HC′P подобны. Значит, когда точка P равномерно движется по отрезку AB, точка Q также равномерно движется по AC, а тогда и точка K движется по некоторому отрезку. Поскольку

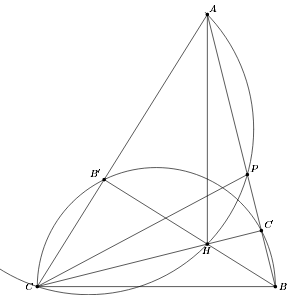
 ∠AHC′ = ∠C > ∠A = ∠CHB′  и  ∠AHB′ > ∠BHC′,  крайние точки этого отрезка соответствуют совпадению точки P с B или Q с C. Рассмотрим для определенности последний случай (см. рис.).

  В этом случае  ∠HCP= ∠HAP= ∠HCB,  то есть треугольникBCPравнобедренный и расстояние отKдо серединыBCравноBC'. Поскольку ∠B> 60°, BC'< ½BC  иKлежит внутри окружности с диаметромBC. Аналогично внутри этой окружности лежит второй конец отрезка, по которому движется точкаK, а следовательно, и весь этот отрезок.

Ответ задачи отсутствует