Задача
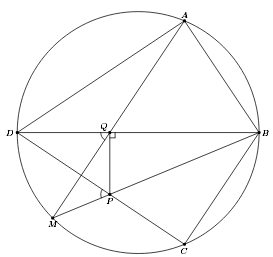
Четырёхугольник ABCD, в котором AB = BC и AD = CD, вписан в окружность. Точка M лежит на меньшей дуге CD этой окружности. Прямые BM и CD пересекаются в точке P, а прямые AM и BD – в точке Q. Докажите, что PQ || AC.
Решение
∠MPD = ∠MBD + ∠BDC = ∠MAD + ∠ADB = ∠MQD. Следовательно, четырёхугольник MPQD – вписанный (см. рис.), а поскольку
∠DMP = ∠DMB = 90°, то PQ ⊥ BD и, значит, PQ || AC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет