Пусть A' – середина дуги BC. Так как  OA' || IA₂,  прямые OI и A'A₂ пересекаются в точке K – центре гомотетии описанной и вписанной окружностей (см. рис.). Докажем, что K – искомый радикальный центр.   Первый способ. Так как инверсия с центром A' и радиусом A'B меняет местами прямую BC и описанную окружность Ω треугольника ABC, точка A₁ переходит в A, а A₂ – в точку A'' пересечения прямой A'A₂ с описанной окружностью. Следовательно, точки A, A₁, A₂ и A'' лежат на одной окружности.

  Степень точкиKотносительно описанной окружности треугольникаAA₁A₂равна  –KA₂·KA'' = – ^r/_R AA'·KA'' = ^r/_R s(K),  гдеs(K)  – степень точкиKотносительно Ω.   Очевидно, степени точкиKотносительно описанных окружностей треугольниковBB₁B₂иCC₁C₂будут такими же, то естьK– радикальный центр трёх окружностей.   Второй способ. Пусть A', B', C' – середины дуг BC, CA, AB. Тогда треугольник A'B'C' переводится в A₂B₂C₂ гомотетией с коэффициентом ^r/_R и центром K, то есть  KA₂ : A'A₂ = KB₂ : B'B₂ = KC₂ : C'C₂ = k : 1.  Для точек прямой A'A₂ разность степеней относительно описанной окружности треугольника AA₁A₂ и вписанной окружности треугольника ABC является линейной функцией. В точке A₂ эта функция равна нулю,

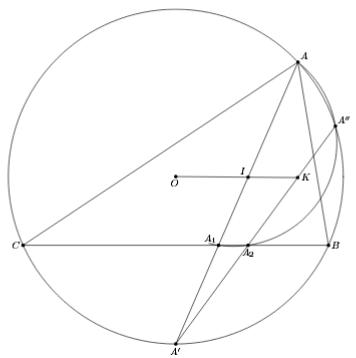
а в точке A'  – r²,  поскольку  A'A₁·A'A = A'B² = A'I²  (первое равенсто следует из подобия треугольников A'A₁B и A'BA, а второе – из леммы о трезубце – см. задачу 153119). Значит, в точке K эта разность равна  – kr².  Другие аналогичные разности в точке K также равны  – kr²,  откуда и следует требуемое.

Ответ задачи отсутствует