Задача
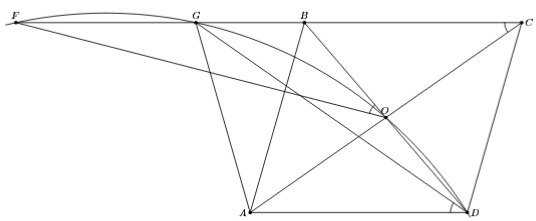
Диагонали параллелограмма ABCD пересекаются в точке O. Касательная, проведённая к описанной окружности треугольника BOC в точке O, пересекает луч CB в точке F. Описанная окружность треугольника FOD повторно пересекает прямую BC в точке G. Докажите, что AG = AB.
Решение
Из условия следует, что ∠GCA = ∠BCO = ∠FOB = 180° – ∠FOD = 180° – ∠FGD = ∠DGC. Следовательно, AGCD – равнобокая трапеция и
AG = DC = AB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет