Задача
В треугольнике ABC ∠A = 60°, точки M и N на сторонах AB и AC соответственно таковы, что центр описанной окружности треугольника ABC делит отрезок MN пополам. Найдите отношение AN : MB.
Решение
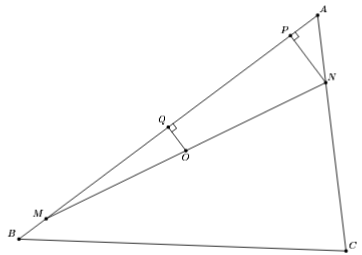
Решение 1:Пусть P, Q – проекции соответственно точки N и центра O описанной окружности на AB (см. рис.). Тогда по условию MQ = QP. С другой стороны, Q – середина AB, следовательно, BM = AP = AN/2 (поскольку в прямоугольном треугольнике APN ∠A = 60°).
Решение 2:Пусть P – точка на описанной окружности треугольника ABC, диаметрально противоположная точке A. Точка O делит пополам отрезки AP и MN, значит, AMPN – параллелограмм. Углы A и BMP равны, так как AC || MP. Угол ABP прямой, так как опирается на диаметр AP. Итак, треугольник BMP прямоугольный с углом 60°, значит, AN = MP = 2MB.
Ответ
2 : 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь