Задача
Выпуклый шестиугольник A1A2...A6 описан около окружности ω радиуса 1. Рассмотрим три отрезка, соединяющие середины противоположных сторон шестиугольника. Для какого наибольшего r можно утверждать, что хотя бы один из этих отрезков не короче r?
Решение
Пусть O – центр окружности ω, а Mi – середина AiAi+1 (считаем, что A7 = A1).
Пример. Если взять точки A1, A2, A3 близкими к вершинам правильного треугольника, а A4, A5 и A6 – близкими к середине A1A3, то длины отрезков M1M4, M2M5 и M3M6 будут близки к 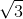 .
.
Оценка. Заметим, что O лежит внутри шестиугольника M1M2...M6. Действительно, если O лежит, например, внутри треугольника M1A1M6, то ω лежит внутри треугольника A2A1A6 и не может касаться всех сторон шестиугольника A1A2...A6.
Будем считать, что вершины исходного шестиугольника упорядочены против часовой стрелки. Обозначим через ∠(AB, CD) угол, на который надо повернуть вектор 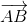 вокруг A против часовой стрелки, чтобы получить вектор, сонаправленный с
вокруг A против часовой стрелки, чтобы получить вектор, сонаправленный с 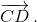
Так как Mi лежит вне ω, то OMi ≥ 1. Значит, если 120° ≤ ∠(OMi, OMi+3) ≤ 240° для некоторого i, то MiMi+3 ≥ 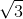 .
.
Предположим, что это условие не выполнено ни для какого i. Пусть j таково, что ∠(OMj, OMj+3) ≤ 120° и ∠(OMj+3, OMj) ≥ 240°. Тогда найдётся такое k, j ≤ k ≤ j + 2, что ∠(OMk, OMk+3) ≤ 120° и ∠(OMk+1, OMk+4) ≥ 240°. Без ограничения общности можно считать, что k = 4. Тогда
120° ≤ ∠M1OM2 ≤ 180° и, значит, M1M2 ≥  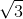 .
.
Рассмотрим выпуклый четырёхугольник M1M2M4M5. Если угол M1 не острый, то
M2M5 > M1M2 ≥ 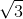 . Если угол M2 не острый, то M1M4 > M1M2 ≥
. Если угол M2 не острый, то M1M4 > M1M2 ≥ 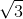 . Пусть оба угла M1 и M2 острые. Тогда 90° < ∠(M1M2, M4M5) < 270°. Так как
. Пусть оба угла M1 и M2 острые. Тогда 90° < ∠(M1M2, M4M5) < 270°. Так как 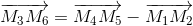 (потому что
(потому что 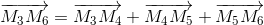 и
и 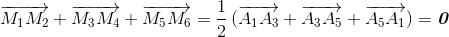 ), то M3M6 > M1M2 ≥
), то M3M6 > M1M2 ≥ 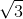 , что и требовалось.
, что и требовалось.
Ответ
r = 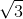 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь