Назад
Задача 166217 • Сложность: 2 • 8-10 класс
Задача

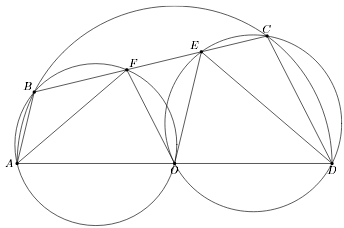
На окружности радиуса R с диаметром AD и центром O выбраны точки B и С по одну сторону от этого диаметра. Около треугольников ABO и CDO описаны окружности, пересекающие отрезок BC в точках F и E. Докажите, что  AF·DE = R².

Авторы:
Москвитин Н. А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина XIII Олимпиада по геометрии имени И.Ф. Шарыгина (2017 г.)
Количество версий:
4
Решение

  Из вписанности четырёхугольника ABFO и равенства  AO = OB  получаем (см. рис.)

AF : R = AF : AO = sin∠AOF : sin∠ABO = sin∠ABF : sin∠ABO = sin∠ABC : sin∠BAD.

  Аналогично  DE:R= sin∠BCD: sin∠CDA.  Так как четырёхугольникABCDвписанный, произведение этих отношений равно 1.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет