Задача
Две окружности пересекаются в точках A и B. Третья окружность касается их обеих и пересекает прямую AB в точках C и D.
Докажите, что касательные к ней в этих точках параллельны общим касательным к двум первым окружностям.
Решение
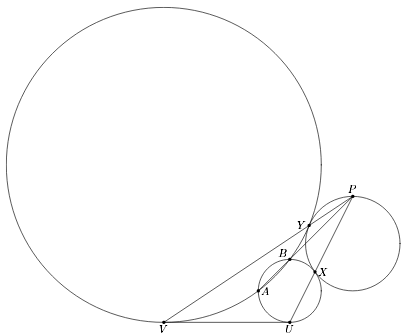
Пусть третья окружность Ω касается двух первых в точках X, Y, а общая касательная – в точках U, V (X и U на одной окружности). Так как X – центр гомотетии касающихся окружностей, прямая XU пересекает Ω в точке P, касательная в которой параллельна UV. Прямая YV также пересекает Ω в точке, касательная в которой параллельна UV, то есть в той же точке P (см. рис.). Кроме того, угол UVY равен углу между YP и касательной к Ω в точке P, то есть углу YXP. Значит, точки X, Y, U, V лежат на одной окружности, так что PX·PU = PY·PV. Следовательно, P лежит на прямой AB и поэтому совпадает с одной из точек C, D. Для второй точки доказательство аналогично.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь