Задача
В прямоугольном треугольнике ABC точка C0 – середина гипотенузы AB, AA1, BB1 – биссектрисы, I – центр вписанной окружности.
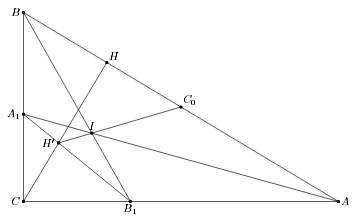
Докажите, что прямые C0I и A1B1 пересекаются на высоте CH.
Решение
Обозначим точку пересечения C0I и CH через H' (см. рис.). Согласно задаче 153133 CH' = r, поэтому расстояния da, db, dc от H' до прямых BC, AC и AB равны соответственно r cos ∠HCB = r cos∠B = r·AC/AB, r·BC/AB и dc = CH – r. Из равенств (AB + BC + CA)r = 2SABC = AB·CH следует, что dc = da + db. Очевидно, что этим свойством обладают также расстояния от точек A1, B1 до прямых BC, CA и AB. Из теоремы Фалеса следует, что все точки, обладающие этим свойством, лежат на прямой A1B1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь