Задача
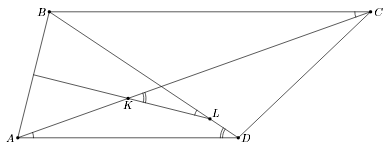
Дана трапеция ABCD с основанием AD. Центр описанной окружности треугольника ABC лежит на прямой BD.
Докажите, что центр описанной окружности треугольника ABD лежит на прямой AC.
Решение
Пусть серединный перпендикуляр к AB пересекает BD и AC в точках K и L соответственно. Тогда из условия следует, что ∠BLK = ∠ACB = ∠CAD. Значит, ∠CKL = ∠BDA, что равносильно утверждению задачи (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет