Решение 1:   Так как центр O описанной окружности принадлежит данному треугольнику ABC, этот треугольник не может быть тупоугольным. Если он прямоугольный, то центр описанной окружности точка O совпадает с серединой гипотенузы, и она совпадает с точкой касания вписанной окружности. Значит, треугольник прямоугольный равнобедренный и утверждение выполнено.

  Далее считаем, что треугольник остроугольный и O лежит на одной из трёх дуг между точками касания. Пусть эта дуга обращена к вершине A. Опустим из O перпендикуляры OD и OE на AB и AC. Основание каждого из них (середина стороны) лежит между A и точкой касания вписанной окружности ω со стороной. Следовательно,  AB > BC  и  AC > BC.

  Теперь достаточно доказать, что отношение любой из сторон AB, AC к BC меньше 2. Пусть D – середина AB, K и L – точки касания ω с AB и BC. Тогда  BK = BL,  и надо доказать, что  DK < CL.  Перпендикуляр DO к AB пересекает ω в точке O, поэтому DK не больше радиуса r окружности ω. С другой стороны,  CL > r,  так как перпендикуляр, восставленный из C к BC, не имеет общих точек с ω (угол C – острый). Следовательно,

BD = BK + KD < BL + LC = BC,  что и требовалось.

Решение 2:   Пусть R, r – радиусы описанной и вписанной окружностей. По формуле Эйлера (см. задачу 152464) получаем, что 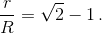   Каждая из сторон треугольника является хордой описанной окружности, касающейся вписанной. Максимальная из таких хорд равна 2R, а минимальная, касающаяся вписанной окружности в точке, противоположной O, равна  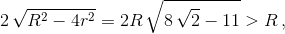  поскольку подкоренное выражение больше ¼.

Ответ задачи отсутствует